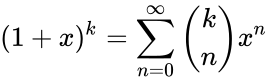Manuals/calci/BINOMIALSERIES

BINOMIALSERIES (N,X,Y)

• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_1,n_2,n_3...} are any real numbers.

Description

• This function gives the coefficient of the Binomial series.
• BinomialSeries is also called Maclaurin series for the function f given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=(1+x)^{\alpha}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} is belongs to any Complex number.
• In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BINOMIALSERIES(N,X,Y)} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} is any positive integer and x and y are any real numbers.
• If k is any number and |x|<1 then,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1+x)^k= \sum_{n=0}^\infty \binom{k}{n} x^n}

 whereFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle  \binom{k}{n} = \frac{k(k-1)(k-2)...(k-n+1)}{n!} }
,n=1,2,3...

• So similar to the binomial theorem except that it’s an infinite series and we must have in order to get convergence.
• This function will give the result as error when

1. N is not positive number.
2. N,X and Y is a Non-numeric.

Examples

1. BINOMIALSERIES(7,2,3)

1	2	0	3	7
7	2	1	3	6
21	2	2	3	5
35	2	3	3	4
35	2	4	3	3
21	2	5	3	2
7	2	6	3	1
1	2	7	3	0

2. BINOMIALSERIES(4,7,16)

1	7	0	16	4
4	7	1	16	3
6	7	2	16	2
4	7	3	16	1
1	7	4	16	0

Related Videos

Binomial Series

See Also

• BINOMIAL
• BINOMIALDISTRIBUTED

References

Binomial Series

• List of Main Z Functions

• Z3 home