Difference between revisions of "Manuals/calci/HYPOTENUSE"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''HYPOTENUSE( | + | <div style="font-size:30px">'''HYPOTENUSE(A,B)'''</div><br/> |
| − | *<math> | + | *<math>A</math> is the value of the opposite side. |
| − | *<math> | + | *<math>B</math> is the adjacent side value. |
| + | **HYPOTENUSE(),returns the hypotenuse side | ||
==Description== | ==Description== | ||
| Line 7: | Line 8: | ||
*A hypotenuse is the longest side of a right-angled triangle. | *A hypotenuse is the longest side of a right-angled triangle. | ||
*The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides. | *The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides. | ||
| − | *In <math>HYPOTENUSE( | + | *In <math>HYPOTENUSE(A,B)</math>, <math>A</math> and <math>B</math> are the lengths of the other two sides of a right angled triangle. |
| − | *<math> | + | *<math>A</math> is the value of the opposite side and <math>B</math> is the value of the adjacent side. |
*So <math>Hypotenuse=\sqrt{a^2+b^2}</math>. | *So <math>Hypotenuse=\sqrt{a^2+b^2}</math>. | ||
This function will return the result as error when any one of the argument is non-numeric. | This function will return the result as error when any one of the argument is non-numeric. | ||
Revision as of 16:18, 2 July 2018
HYPOTENUSE(A,B)
- is the value of the opposite side.
- is the adjacent side value.
- HYPOTENUSE(),returns the hypotenuse side
Description
- This function gives the value of the hypotenuse side.
- A hypotenuse is the longest side of a right-angled triangle.
- The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides.
- In , and are the lengths of the other two sides of a right angled triangle.
- is the value of the opposite side and is the value of the adjacent side.
- So .
This function will return the result as error when any one of the argument is non-numeric.
Examples
- =HYPOTENUSE(6,8) = 10
- =HYPOTENUSE(1,0) = 1
- =HYPOTENUSE(2.5,6.2) = 6.68505796534
- =HYPOTENUSE(12,20) = 23.32350787
- =HYPOTENUSE(-2,4) = 4.472135954999
- =HYPOTENUSE(-3,-4) = 5
Related Videos
See Also
References
 is the value of the opposite side.
is the value of the opposite side. is the adjacent side value.
is the adjacent side value.
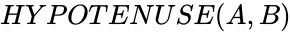 ,
, 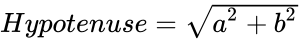 .
.