Difference between revisions of "Manuals/calci/BIRTHDAYPROBABILITY"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''BIRTHDAYPROBABILITY (NumberOfDuplicates,TotalNumberOfDays)'''</div><br/> *<math>NumberOfDuplicates</math> is any real number. *<math>TotalNumbe...") |
|||
| Line 19: | Line 19: | ||
==See Also== | ==See Also== | ||
| − | *[[Manuals/calci/ | + | *[[Manuals/calci/GENERATESUDOKU | GENERATESUDOKU ]] |
| + | *[[Manuals/calci/MAGICSQUARE | MAGICSQUARE ]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://mathforum.org/dr.math/faq/faq.birthdayprob.html Birthday Probability] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Revision as of 15:09, 26 July 2017
BIRTHDAYPROBABILITY (NumberOfDuplicates,TotalNumberOfDays)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NumberOfDuplicates} is any real number.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle TotalNumberOfDays} is the number of days.
Description
- This function shows the value of the Birthday probability.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BIRTHDAYPROBABILITY (NumberOfDuplicates,TotalNumberOfDays)} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number of Duplicates} is the additional number of birthday.
- is the number of days.
- Birthday probability is the sum of the probability that an event will happen and the probability that the event won't happen is always 1.
- In a room of 75 there is a 99.9% chance of two people birthday matching.
- To work out the probability there is no two people will have the same birthday,the following rules to be followed to find the probability that two people will share a birthday:
P(two people share birthday) + P(no two people share birthday) = 1 P(two people share birthday) = 1 - P(no two people share birthday).
Examples
- BIRTHDAYPROBABILITY(3,30) = 0.1384203445582639
- BIRTHDAYPROBABILITY(20,432) = 0.3686145731391096
- BIRTHDAYPROBABILITY(30.3,765) = 0.44899395029084743
See Also
References
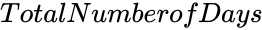 is the number of days.
is the number of days.