Difference between revisions of "Manuals/calci/WEIBULL"
Jump to navigation
Jump to search
| Line 15: | Line 15: | ||
*<math>Cumulative</math> is the logical value which determines the form of the distribution. | *<math>Cumulative</math> is the logical value which determines the form of the distribution. | ||
*When <math>Cumulative</math> is TRUE, this function gives the value of the cumulative distribution. When <math>Cumulative</math> is FALSE, then this function gives the value of the probability density function. | *When <math>Cumulative</math> is TRUE, this function gives the value of the cumulative distribution. When <math>Cumulative</math> is FALSE, then this function gives the value of the probability density function. | ||
| − | *When we are not omitting the value of <math> | + | *When we are not omitting the value of <math>Cumulative</math>, then it consider as FALSE. |
*Weibull distribution is of two type :3-parameter weibull distribution and 2-parameter weibull distribution. | *Weibull distribution is of two type :3-parameter weibull distribution and 2-parameter weibull distribution. | ||
*This function gives the value of 2-parameter weibull distribution by setting the third parameter (location parameter) is zero. | *This function gives the value of 2-parameter weibull distribution by setting the third parameter (location parameter) is zero. | ||
Revision as of 15:04, 18 June 2018
WEIBULL(x,alpha,beta,lv)
(Number,Alpha,Beta,Cumulative)
- is the value of the function.
- and are the parameter of the distribution.
- is the logical value.
Description
- This function gives the value of the weibull distribution with 2-parameters.
- It is a continuous probability distribution.
- Weibull distribution also called Rosin Rammler distribution.
- It is used to model the lifetime of technical devices and is used to describe the particle size distribution of particles generated by grinding, milling and crushing operations.
- This distribution is closely related to the lognormal distribution.
- In , is the value to evaluate the function.
- is the shape parameter of the distribution. is the scale parameter of the distribution.
- is the logical value which determines the form of the distribution.
- When is TRUE, this function gives the value of the cumulative distribution. When is FALSE, then this function gives the value of the probability density function.
- When we are not omitting the value of , then it consider as FALSE.
- Weibull distribution is of two type :3-parameter weibull distribution and 2-parameter weibull distribution.
- This function gives the value of 2-parameter weibull distribution by setting the third parameter (location parameter) is zero.
- Also if alpha<1,then the failure rate of the device decreases over time.
- If alpha=1, then the failure rate of the device is constant over time.
- If alpha>1, then the failure rate of the device increases over time.
- The equation for cumulative distribution function is: =.
- The equation for probability density function is:
- When alpha =1, then this function gives the exponential with .
- This function gives the result as error when
1. Any one of the argument is non-numeric. 2. Number is negative. 3. Alpha or Beta
Examples
- =WEIBULL(202,60,81,TRUE) = 1
- =WEIBULL(202,60,81,FALSE) = 0
- =WEIBULL(160,80,170,TRUE) = 0.00779805060
- =WEIBULL(160,80,170,FALSE) = 0.0038837823333
- = WEIBULL(10.5,2.1,5.3,TRUE) = 0.9850433821261
- =WEIBULL(10.5,2.1,5.3,FALSE) = 0.0125713406729
Related Videos
See Also
References
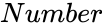 is the value of the function.
is the value of the function.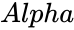 and
and 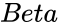 are the parameter of the distribution.
are the parameter of the distribution.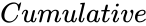 is the logical value.
is the logical value. ,
,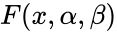 =
=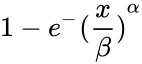 .
.
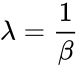 .
.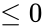 or Beta
or Beta