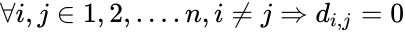Difference between revisions of "Manuals/calci/DIAGONALMATRIX"
Jump to navigation
Jump to search
| Line 5: | Line 5: | ||
==Description== | ==Description== | ||
*This function shows the Diagonal matrix of a given order. | *This function shows the Diagonal matrix of a given order. | ||
| − | *In <math> | + | *In <math>MATRIX (TypeOfMatrix,DimensionsOfMatrix,SeedValuesToUse,IJFunction,PreParameter,IsItInternalCall</math>, <math>DimensionsOfMatrix</math> is the order of square matrix. |
*A diagonal matrix is a square matrix which is of the form <math>a_{ij}=c_{i} \delta_{ij}</math> where <math>\delta_{ij}</math> is the Kronecker delta, <math>c_{i}</math> are constants, and i,j=1, 2, ..., n. | *A diagonal matrix is a square matrix which is of the form <math>a_{ij}=c_{i} \delta_{ij}</math> where <math>\delta_{ij}</math> is the Kronecker delta, <math>c_{i}</math> are constants, and i,j=1, 2, ..., n. | ||
*The general diagonal matrix is of the form: | *The general diagonal matrix is of the form: | ||
Revision as of 12:42, 15 August 2018
MATRIX (TypeOfMatrix,DimensionsOfMatrix,SeedValuesToUse,IJFunction,PreParameter,IsItInternalCall)
- is the type of the matrix.
- is the order of the diagonal matrix.
Description
- This function shows the Diagonal matrix of a given order.
- In , is the order of square matrix.
- A diagonal matrix is a square matrix which is of the form where is the Kronecker delta, are constants, and i,j=1, 2, ..., n.
- The general diagonal matrix is of the form:
- So the main diagonal entries are need not to be zero and off-diagonal entries are zero.
- That is,the matrix D = (di,j) with n columns and n rows is diagonal if:
Examples
See Also
References
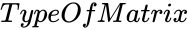 is the type of the matrix.
is the type of the matrix.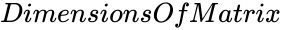 is the order of the diagonal matrix.
is the order of the diagonal matrix.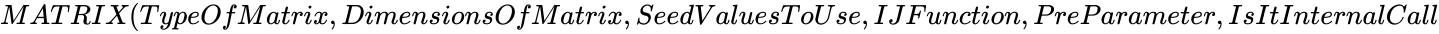 ,
, 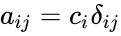 where
where 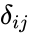 is the Kronecker delta,
is the Kronecker delta, 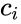 are constants, and i,j=1, 2, ..., n.
are constants, and i,j=1, 2, ..., n.