Difference between revisions of "Manuals/calci/GOLDENRATIO"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''GOLDENRATIO'''(phismall) where '''phismall''' is true or false </div> ---- <div id="1SpaceContent" cl...") |
|||
| Line 1: | Line 1: | ||
| − | + | =GOLDENRATIO(phismall)= | |
| − | + | *where <math>phismall</math> is the logical value TRUE or FALSE. | |
| − | + | GOLDENRATIO() returns the golden ratio value. | |
| − | + | == Description == | |
| − | + | *Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. | |
| − | + | *Golden ratio is represented as '''phi(φ)''' and its conjugate is represented as '''Phi (&Phi)'''. | |
| − | + | *If 'a' and 'b' are two quantities with 'a>b', then | |
| − | + | (φ) = <math>\frac{\(a + b)}{a}</math> = <math>\frac{\a}{b}</math> | |
| + | *Using quadratic formula, golden ratio is represented as - | ||
| − | </ | + | φ = <math>\frac{1+&sqrt; 5}{2}</math> = 1.618033988749895 |
| − | |||
| − | |||
| − | + | Φ = <math>\frac{1-&sqrt; 5}{2}</math> = 0.6180339887498948 | |
| − | </ | + | *Argument <math>phismall</math> can be logical values TRUE (or 1) or FALSE (or 0). Any other argument values are ignored and Calci assumes it to be TRUE or 1. |
| − | + | *If argument <math>phismall</math> is omitted, Calci assumes it as TRUE or 1 and displays the output as ''0.6180339887498948''. | |
| − | < | + | *If argument is invalid, Calci returns a #NULL error message. |
| − | + | == Examples == | |
| − | + | GOLDENRATIO(TRUE) ''returns 0.6180339887498948'', value of capitalphi Φ | |
| − | |||
| − | |||
| − | + | GOLDENRATIO(1) ''returns 0.6180339887498948'', value of capitalphi Φ | |
| − | + | GOLDENRATIO(FALSE) ''returns 1.618033988749895'', value of smallphi φ | |
| − | + | GOLDENRATIO() ''returns 0.6180339887498948'', value of capitalphi Φ | |
| − | + | == See Also == | |
| − | + | *[[Manuals/calci/GOLDENANGLE | GOLDENANGLE]] | |
| − | + | == References == | |
| − | + | *[http://en.wikipedia.org/wiki/Golden_ratio Golden Ratio] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 07:17, 19 December 2013
GOLDENRATIO(phismall)
- where is the logical value TRUE or FALSE.
GOLDENRATIO() returns the golden ratio value.
Description
- Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities.
- Golden ratio is represented as phi(φ) and its conjugate is represented as Phi (&Phi).
- If 'a' and 'b' are two quantities with 'a>b', then
(φ) = Failed to parse (syntax error): {\displaystyle \frac{\(a + b)}{a}}
= Failed to parse (unknown function "\a"): {\displaystyle \frac{\a}{b}}
- Using quadratic formula, golden ratio is represented as -
φ = Failed to parse (syntax error): {\displaystyle \frac{1+&sqrt; 5}{2}} = 1.618033988749895
Φ = Failed to parse (syntax error): {\displaystyle \frac{1-&sqrt; 5}{2}} = 0.6180339887498948
- Argument can be logical values TRUE (or 1) or FALSE (or 0). Any other argument values are ignored and Calci assumes it to be TRUE or 1.
- If argument is omitted, Calci assumes it as TRUE or 1 and displays the output as 0.6180339887498948.
- If argument is invalid, Calci returns a #NULL error message.
Examples
GOLDENRATIO(TRUE) returns 0.6180339887498948, value of capitalphi Φ
GOLDENRATIO(1) returns 0.6180339887498948, value of capitalphi Φ
GOLDENRATIO(FALSE) returns 1.618033988749895, value of smallphi φ
GOLDENRATIO() returns 0.6180339887498948, value of capitalphi Φ
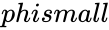 is the logical value TRUE or FALSE.
is the logical value TRUE or FALSE.