Difference between revisions of "Manuals/calci/NORMDIST"
Jump to navigation
Jump to search
'
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"><font color="#000000"><font face="Arial, sans-serif"><font size="2">'''NORMDIST'''</font></font><font face="Arial, sans-s...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''NORMDIST(x,m,sd,cu)'''</div><br/> |
| + | *<math>x</math> is the value,<math>m</math> is the mean,<math>sd</math> is the standard deviation and <mathcu</math> is the logical value like TRUE or FALSE. | ||
| − | < | + | ==Description== |
| + | *This function gives the normal distribution for the particular mean and standard deviation. | ||
| + | *Normal distribution is the function that represents the distribution of many random variables as a symmetrical bell-shaped graph. | ||
| + | *This distribution is the continuous probability distribution.It is also called Gaussian distribution. | ||
| + | *In <math> NORMDIST(x,m,sd,cu) ,x</math> is the value of the function,<math> m</math> is the arithmetic mean of the distribution, <math>sd</math> is the standard deviation of the distribution and <math>cu</math> is the logical value that indicating the form of the function. | ||
| + | *Suppose cu is TRUE, this function gives the cumulative distribution, and it is FALSE, this function give the probability mass function. | ||
| + | *The equation for the normal distribution is: f(x,μ,σ)=1/σsqrt(2pi()).e^-{(x-μ)^2/2σ^2}, where \mu is the mean of the distribution,\sigma is the standard deviation of the distribution. | ||
| + | *In this formula, Suppose \mu = 0 and \sigma = 1, then the distribution is called the standard normal distribution or the unit normal distribution. | ||
| + | *This function will return the result as error when any one of the argument is nonnumeric and sd<=0. | ||
| + | when cu is TRUE , this formula is the integral from -infinity to x and cu is FALSE , we can use the same formula. | ||
| + | |||
| + | font><font face="Arial, sans-serif"><font size="2">'''sd'''</font></font><font face="Arial, sans-serif"><font size="2"> is the standard deviation of the distribution.</font></font></font> | ||
<font color="#000000"><font face="Arial, sans-serif"><font size="2">'''c'''</font></font><font face="Arial, sans-serif"><font size="2"> is a logical value that determines the form of the function. </font></font></font> | <font color="#000000"><font face="Arial, sans-serif"><font size="2">'''c'''</font></font><font face="Arial, sans-serif"><font size="2"> is a logical value that determines the form of the function. </font></font></font> | ||
| Line 38: | Line 50: | ||
<font color="#000000"><font face="Times New Roman, serif"><font size="3">i.e. </font></font></font><font color="#000000"><font face="Trebuchet MS, sans-serif"><font size="3">=NORMDIST (52, 50, 2.5, true)</font></font></font><font color="#000000"><font face="Times New Roman, serif"><font size="3"> is 0.7885</font></font></font> | <font color="#000000"><font face="Times New Roman, serif"><font size="3">i.e. </font></font></font><font color="#000000"><font face="Trebuchet MS, sans-serif"><font size="3">=NORMDIST (52, 50, 2.5, true)</font></font></font><font color="#000000"><font face="Times New Roman, serif"><font size="3"> is 0.7885</font></font></font> | ||
| − | <font color="#000000"><font face="Trebuchet MS, sans-serif"><font size="3"> | + | <font color="#000000"><font face="Trebuchet MS, sans-serif"><font size="3">UNIQcc0d9c136de91e77-nowiki-00000002-QINU</font></font></font><font color="#000000"><font face="Times New Roman, serif"><font size="3"> is 0.1159.</font></font></font> |
</div> | </div> | ||
Revision as of 02:27, 1 January 2014
NORMDIST(x,m,sd,cu)
- is the value, is the mean, is the standard deviation and <mathcu</math> is the logical value like TRUE or FALSE.
Description
- This function gives the normal distribution for the particular mean and standard deviation.
- Normal distribution is the function that represents the distribution of many random variables as a symmetrical bell-shaped graph.
- This distribution is the continuous probability distribution.It is also called Gaussian distribution.
- In is the value of the function, is the arithmetic mean of the distribution, is the standard deviation of the distribution and is the logical value that indicating the form of the function.
- Suppose cu is TRUE, this function gives the cumulative distribution, and it is FALSE, this function give the probability mass function.
- The equation for the normal distribution is: f(x,μ,σ)=1/σsqrt(2pi()).e^-{(x-μ)^2/2σ^2}, where \mu is the mean of the distribution,\sigma is the standard deviation of the distribution.
- In this formula, Suppose \mu = 0 and \sigma = 1, then the distribution is called the standard normal distribution or the unit normal distribution.
- This function will return the result as error when any one of the argument is nonnumeric and sd<=0.
when cu is TRUE , this formula is the integral from -infinity to x and cu is FALSE , we can use the same formula.
font>sd is the standard deviation of the distribution.
c is a logical value that determines the form of the function.
It calculates the normal distribution for the specified mean and standard deviation.
· NORMDIST displays error for nonnumeric sd.
- When sd <=0, NORMDIST displays error.
- The equation for the normal density function (cumulative = FALSE) is:
NORMDIST
Let’s see an example in (Column1 Row 1, Column1Row2, Column1Row3)
NORMDIST (C1R1, C1R2, C1R3)
i.e. =NORMDIST (52, 50, 2.5, true) is 0.7885
?UNIQcc0d9c136de91e77-nowiki-00000002-QINU? is 0.1159.
Syntax
Remarks
Examples
Description
| Column1 | Column2 | Column3 | Column4 | |||
| Row1 | 52 | 0.7885 | 0.1159 | |||
| Row2 | 50 | |||||
| Row3 | 2.5 | |||||
| Row4 | ||||||
| Row5 | ||||||
| Row6 |
 is the value,
is the value, is the mean,
is the mean,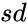 is the standard deviation and <mathcu</math> is the logical value like TRUE or FALSE.
is the standard deviation and <mathcu</math> is the logical value like TRUE or FALSE.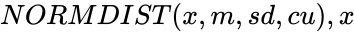 is the value of the function,
is the value of the function,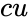 is the logical value that indicating the form of the function.
is the logical value that indicating the form of the function.