Difference between revisions of "Manuals/calci/NORMDIST"
Jump to navigation
Jump to search
| Line 8: | Line 8: | ||
*In <math> NORMDIST(x,m,sd,cu) ,x</math> is the value of the function,<math> m</math> is the arithmetic mean of the distribution, <math>sd</math> is the standard deviation of the distribution and <math>cu</math> is the logical value that indicating the form of the function. | *In <math> NORMDIST(x,m,sd,cu) ,x</math> is the value of the function,<math> m</math> is the arithmetic mean of the distribution, <math>sd</math> is the standard deviation of the distribution and <math>cu</math> is the logical value that indicating the form of the function. | ||
*Suppose cu is TRUE, this function gives the cumulative distribution, and it is FALSE, this function give the probability mass function. | *Suppose cu is TRUE, this function gives the cumulative distribution, and it is FALSE, this function give the probability mass function. | ||
| − | *The equation for the normal distribution is: <math> f(x,\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}.e^-\left({\frac{(x-\mu)^2}{2\sigma^2}}\right)</math>, where \mu is the mean of the distribution,\sigma is the standard deviation of the distribution. | + | *The equation for the normal distribution is: <math> f(x,\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}.e^-\left({\frac{(x-\mu)^2}{2\sigma^2}}\right)</math>, where <math>\mu</math> is the mean of the distribution,<math>\sigma</math> is the standard deviation of the distribution. |
| − | *In this formula, Suppose \mu = 0 and \sigma = 1, then the distribution is called the standard normal distribution or the unit normal distribution. | + | *In this formula, Suppose <math>\mu</math> = 0 and <math>\sigma</math>= 1, then the distribution is called the standard normal distribution or the unit normal distribution. |
*This function will return the result as error when any one of the argument is nonnumeric and sd<=0. | *This function will return the result as error when any one of the argument is nonnumeric and sd<=0. | ||
when cu is TRUE , this formula is the integral from -infinity to x and cu is FALSE , we can use the same formula. | when cu is TRUE , this formula is the integral from -infinity to x and cu is FALSE , we can use the same formula. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 03:30, 1 January 2014
NORMDIST(x,m,sd,cu)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is the value,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} is the mean,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sd} is the standard deviation and is the logical value like TRUE or FALSE.
Description
- This function gives the normal distribution for the particular mean and standard deviation.
- Normal distribution is the function that represents the distribution of many random variables as a symmetrical bell-shaped graph.
- This distribution is the continuous probability distribution.It is also called Gaussian distribution.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NORMDIST(x,m,sd,cu) ,x} is the value of the function,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} is the arithmetic mean of the distribution, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sd} is the standard deviation of the distribution and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cu} is the logical value that indicating the form of the function.
- Suppose cu is TRUE, this function gives the cumulative distribution, and it is FALSE, this function give the probability mass function.
- The equation for the normal distribution is: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x,\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}.e^-\left({\frac{(x-\mu)^2}{2\sigma^2}}\right)} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} is the mean of the distribution,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} is the standard deviation of the distribution.
- In this formula, Suppose Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} = 0 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} = 1, then the distribution is called the standard normal distribution or the unit normal distribution.
- This function will return the result as error when any one of the argument is nonnumeric and sd<=0.
when cu is TRUE , this formula is the integral from -infinity to x and cu is FALSE , we can use the same formula.
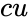 is the logical value like TRUE or FALSE.
is the logical value like TRUE or FALSE.