Difference between revisions of "Manuals/calci/BINOMIALDISTRIBUTED"
Jump to navigation
Jump to search
| Line 23: | Line 23: | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Binomial_distribution Binomial Distribution] | [http://en.wikipedia.org/wiki/Binomial_distribution Binomial Distribution] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Revision as of 01:25, 13 March 2017
BINOMIALDISTRIBUTED (Numbers,Probability)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Numbers} is the number of variables.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Probability} is the value from 0 to 1.
Description
- This function gives the value of the Binomial distribution.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BINOMIALDISTRIBUTED (Numbers,Probability)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Numbers} is the number of the variables and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Probability} is the probability value which varies from 0 to 1.
- This gives the discrete probability distribution.
- The probability of getting exactly k successes in n trials is given by the Probability Mass Function:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b(k;n,p)=Pr(X = k) = \binom{n}{k}p^{k}(1-p)^{n-k}} for k=0,1,2,3...n where is the COMBIN(n,k) i.e.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \binom{n}{k} = \frac{n!}{k!(n-k)}!}
- The Cumulative Binomial Distribution is:Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(x;n,p) = Pr(X \le x) =\sum_{i=0}^x \binom{n}{i}p^{i}(1-p)^{(n-i)}} .
Examples
- BINOMIALDISTRIBUTED(10,0.4) = 0 0 0 0 0 0 0 0
See Also
References
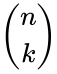 is the COMBIN(n,k) i.e.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \binom{n}{k} = \frac{n!}{k!(n-k)}!}
is the COMBIN(n,k) i.e.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \binom{n}{k} = \frac{n!}{k!(n-k)}!}