Difference between revisions of "Manuals/calci/VECTORPRODUCT"
Jump to navigation
Jump to search
(Created page with "VECTORPRODUCT") |
|||
| Line 1: | Line 1: | ||
| − | VECTORPRODUCT | + | <div style="font-size:30px">'''VECTORPRODUCT (a,b)'''</div><br/> |
| + | *<math>a</math> and <math>b</math> are any real numbers. | ||
| + | |||
| + | ==Description== | ||
| + | *This function shows the Cross product of two numbers. | ||
| + | *Vector product is also called Cross product. | ||
| + | *The Vector product is defined in three dimensional space and it is denoted by axb. | ||
| + | *In VECTORPRODUCT (a,b), a and b are any two positive real numbers. | ||
| + | *We can calculate the Cross Product this way: | ||
| + | *<math>a X b</math> = <math>\mid a\mid</math>.<math> \mid b\mid</math><math> sin(\theta) n</math> | ||
| + | *<math>\mid a\mid</math> is the magnitude (length) of vector a | ||
| + | *<math>\mid b</math> is the magnitude (length) of vector b | ||
| + | *<math>\theta</math> is the angle between a and b | ||
| + | *<math>n</math> is the unit vector at right angles to both a and b. | ||
| + | |||
| + | ==Examples== | ||
| + | #VECTORPRODUCT([2,3,5],[8,6,4]) = -18 32 -12 | ||
| + | #VECTORPRODUCT([4,10,3.2],[9,5.3,4]) = 23.04 12.8 -68.8 | ||
| + | #VECTORPRODUCT([5.3,7.2,8],[-6,-4,7]) = 82.4 -85.1 22.000000000000004 | ||
| + | |||
| + | ==See Also== | ||
Revision as of 14:01, 17 May 2017
VECTORPRODUCT (a,b)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} are any real numbers.
Description
- This function shows the Cross product of two numbers.
- Vector product is also called Cross product.
- The Vector product is defined in three dimensional space and it is denoted by axb.
- In VECTORPRODUCT (a,b), a and b are any two positive real numbers.
- We can calculate the Cross Product this way:
- = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid a\mid} .Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid b\mid} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sin(\theta) n}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid a\mid} is the magnitude (length) of vector a
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid b} is the magnitude (length) of vector b
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} is the angle between a and b
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} is the unit vector at right angles to both a and b.
Examples
- VECTORPRODUCT([2,3,5],[8,6,4]) = -18 32 -12
- VECTORPRODUCT([4,10,3.2],[9,5.3,4]) = 23.04 12.8 -68.8
- VECTORPRODUCT([5.3,7.2,8],[-6,-4,7]) = 82.4 -85.1 22.000000000000004
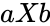 = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid a\mid}
.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid b\mid}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sin(\theta) n}
= Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid a\mid}
.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid b\mid}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sin(\theta) n}