Difference between revisions of "Manuals/calci/LUCAS"
| Line 9: | Line 9: | ||
*The difference between Lucas and Fibonacci numbers are with the first two terms <math>L_0=2</math> and <math>L_1=1 </math>, but <math>F_0=0</math> and <math>F_1=1</math>. | *The difference between Lucas and Fibonacci numbers are with the first two terms <math>L_0=2</math> and <math>L_1=1 </math>, but <math>F_0=0</math> and <math>F_1=1</math>. | ||
*The Lucas numbers are defined by: | *The Lucas numbers are defined by: | ||
| − | <math>L_n=\begin{Bmatrix} 2 & if | + | <math>L_n=\begin{Bmatrix} 2 & if & n=0 \\ |
| − | 1 &if n=1 \\ | + | 1 &if & n=1 \\ |
| − | L_{n-1}+L_{n-2} &if | + | L_{n-1}+L_{n-2} &if & n>1 |
\end{Bmatrix}</math> | \end{Bmatrix}</math> | ||
*The sequence of Lucas numbers is 2,1,3,4,7,11,18,29.... | *The sequence of Lucas numbers is 2,1,3,4,7,11,18,29.... | ||
Revision as of 16:38, 20 July 2017
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } is the number indicating the position.
Description
- This function gives the Lucas series of the numbers.
- Lucas numbers are similar to the Fibonacci numbers.
- It is generated by added the last two numbers in the series.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LUCAS(n)} , is the numbers position, which is used to displaying the numbers in the given range.
- The difference between Lucas and Fibonacci numbers are with the first two terms Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_0=2} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1=1 } , but Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_0=0} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_1=1} .
- The Lucas numbers are defined by:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_n=\begin{Bmatrix} 2 & if & n=0 \\ 1 &if & n=1 \\ L_{n-1}+L_{n-2} &if & n>1 \end{Bmatrix}}
- The sequence of Lucas numbers is 2,1,3,4,7,11,18,29....
- The relation between Lucas and Fibonacci numbers are:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_n=F_n+2F_{n-1} } and : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_n=\frac{L_{n-1}+L_{n+1}}{5}} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} is the Lucas series with is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^{th}} Lucas number and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_n } is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^{th}} Fibonacci number.
This function will, give the result as error when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
is non-numeric or n < 0
Examples
- =LUCAS(5) = 2 1 3 4 7 11
- =LUCAS(0) = 2
- =LUCAS(1) = 2 1
- =LUCAS(3) = 2 1 3 4
- =LUCAS(-1) = Null
Related Videos
See Also
References
 is the numbers position, which is used to displaying the numbers in the given range.
is the numbers position, which is used to displaying the numbers in the given range.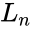 is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^{th}}
Lucas number and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_n }
is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^{th}}
Fibonacci number.
is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^{th}}
Lucas number and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_n }
is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^{th}}
Fibonacci number.