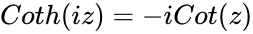Difference between revisions of "Manuals/calci/COTH"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''COTH( | + | <div style="font-size:30px">'''COTH(x)'''</div><br/> |
| − | * where | + | * where x is any real number. |
| + | **COTH() returns the inverse hyperbolic tangent of a number. | ||
| + | |||
==Description== | ==Description== | ||
| − | *This function gives the hyperbolic Cotangent of ' | + | *This function gives the hyperbolic Cotangent of 'x'. |
*It's also called as Circular function. | *It's also called as Circular function. | ||
| + | *Let z is any real number. | ||
*COTH is the reciprocal of TANH function.i.e.COTH(z)=<math>(tanh (z))^{-1}</math> | *COTH is the reciprocal of TANH function.i.e.COTH(z)=<math>(tanh (z))^{-1}</math> | ||
*<math>COTH(z)=\frac{Cosh(z)}{Sinh(z)}</math> i.e <math>\frac {e^z+e^{-z}} {e^z-e^{-z}}</math> or iCOT(iz).where 'i' is the imaginary unit and <math>i=\sqrt{-1}</math>. | *<math>COTH(z)=\frac{Cosh(z)}{Sinh(z)}</math> i.e <math>\frac {e^z+e^{-z}} {e^z-e^{-z}}</math> or iCOT(iz).where 'i' is the imaginary unit and <math>i=\sqrt{-1}</math>. | ||
Revision as of 16:30, 18 June 2018
COTH(x)
- where x is any real number.
- COTH() returns the inverse hyperbolic tangent of a number.
Description
- This function gives the hyperbolic Cotangent of 'x'.
- It's also called as Circular function.
- Let z is any real number.
- COTH is the reciprocal of TANH function.i.e.COTH(z)=
- i.e or iCOT(iz).where 'i' is the imaginary unit and .
- Also relation between Hyperbolic & Trignometric function is &
Examples
COTH(z)
- z is any real number.
| COTH(z) | Value |
| COTH(1) | 1.3130352854993312 |
| COTH(30) | 1 |
| COTH(-45) | -1 |
Related Videos
See Also
References
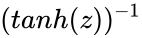
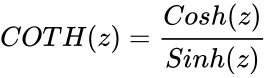 i.e
i.e 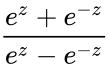 or iCOT(iz).where 'i' is the imaginary unit and
or iCOT(iz).where 'i' is the imaginary unit and 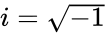 .
.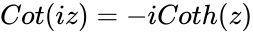 &
&