Manuals/calci/FDIST
Jump to navigation
Jump to search
FDIST(x,df1,df2)
- is the value of the function
- and is degrees of freedom.
Description
- This function gives the value of F probability distribution.
- This distribution is continuous probability distribution and it is called Fisher-Snedecor distribution.
- The F distribution is an asymmetric distribution that has a minimum value of 0, but no maximum value.
- In is the value of the function , is the numerator degrees of freedom and is the denominator degrees of freedom.
- This distribution is the ratio of two chi-square distributions with degrees of freedom r1 and r2, respectively, where each chi-square has first been divided by its degrees of freedom.
- The Probability density function of the F distribution is:
Failed to parse (syntax error): {\displaystyle f(x,r1,r2)=Γ[(r1+r2)/2](r1/r2)^r1/2*(x)r1/2-1/ Γ(r1/2)Γ(r2/2)(1+r1x/r2)^(r1+r2)/2, 0<x<\infty} where Γ is the gamma function.
- The gamma function is defined by Gamma(t) = integral 0 to infinity x^{t-1} e^{-x} dx.
When the value of df1 and df2 are not integers ,then it is converted in to integers.
- This function will give the result as error when
1. any one of the argument is nonnumeric. 2.x is negative 3. df1 or df2<1 ,and df1 ordf2>=10^10
Examples
- FDIST(20.6587,7,3)=0.01526530981
- FDIST(70.120045,12.2,6.35)=0.000011229898
- FDIST(10,1.3,1.5)=0.134947329626
- FDIST(-28,4,6)=NAN
See Also
 is the value of the function
is the value of the function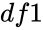 and
and 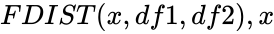 is the value of the function ,
is the value of the function ,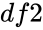 is the denominator degrees of freedom.
is the denominator degrees of freedom.