Manuals/calci/IMARGUMENT
Jump to navigation
Jump to search
IMARGUMENT(z)
- is the complex number is of the form
- is the order of the Bessel function and is an integer
Description
- This function gives the principal value of the argument of the complex-valued expression .
- i.e The angle from the positive axis to the line segment is called the Argument of a complex number.
- In this function angle value is in Radians.
- Here IMARGUMENT(z), Where is the complex number in the form of . i.e & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} are the real numbers.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} imaginary unit .Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=\sqrt(-1)} .
- An argument of the complex number Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = x + iy} is any real quantity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} such that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = x + i y} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r cosφ + i r sinφ} for some positive real number Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} .
- Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = |z| = \sqrt{x^2+y^2}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi \in [(-\Pi(),\Pi()]<math>. *The argument of a complex number is calculated by <math>arg(z)= tan^{-1}(\frac{y}{x}) =\theta<math> in Radians. *To change the Radian value to Degree we can use DEGREES function or we can multiply the answer with <math>\frac{180}{\pi}} .
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
Examples
- IMARGUMENT("3-2i") = -0.588002604
- IMARGUMENT("5+6i") = 0.876058051
- IMARGUMENT("2") = 0
- IMARGUMENT("4i") = 1.570796327
- DEGREES(IMARGUMENT("2+2i")) = 45
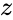 is the complex number is of the form
is the complex number is of the form 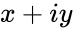
 is the order of the Bessel function and is an integer
is the order of the Bessel function and is an integer & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y}
are the real numbers.
& Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y}
are the real numbers.