Manuals/calci/HILBERT
MATRIX("HILBERT",order)
- is the order of the Hilbert matrix.
Description
- This function gives matrix of order 3x3 with the property of Hilbert.
- A Hilbert matrix, is a square matrix with entries being the unit fractions. i.e.,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{ij}=\frac{1}{i+j-1}. *Example for 5x5 Hilbert matrix is: <math>\begin{bmatrix} 1 & \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} \\ \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} \\ \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7} \\ \frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8} \\ \frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8} & \frac{1}{9} \\ \end{bmatrix}} .
- The Hilbert matrix is an example of a Hankel matrix.
- The Hilbert matrix is symmetric and positive definite.
- Also Hilbert matrices are canonical examples of ill-conditioned matrices, making them notoriously difficult to use in numerical computation.
- Here MATRIX("hilbert") gives the hilbert matrices with a decimal places .
- i.e., For 1/2 it will show 0.5, 1/3 will show 0.333 and so on.
Examples
- 1.MATRIX("hilbert")= 1
- 2.MATRIX("hilbert",3)
| 1 | 0.5 | 0.3333333333333333 |
| 0.5 | 0.3333333333333333 | 0.25 |
| 0.3333333333333333 | 0.25 | 0.2 |
- 3.MATRIX("hilbert",5)
| 1 | 0.5 | 0.3333333333333333 | 0.25 | 0.2 |
| 0.5 | 0.3333333333333333 | 0.25 | 0.2 | 0.16666666666666666 |
| 0.3333333333333333 | 0.25 | 0.2 | 0.16666666666666666 | 0.14285714285714285 |
| 0.25 | 0.2 | 0.16666666666666666 | 0.14285714285714285 | 0.125 |
| 0.2 | 0.16666666666666666 | 0.14285714285714285 | 0.125 | 0.1111111111111111 |
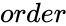 is the order of the Hilbert matrix.
is the order of the Hilbert matrix.