Manuals/calci/ACKERMANN
Jump to navigation
Jump to search
ACKERMANN(m,n)
- and are the positive integers.
Description
- The Ackermann function is a classic example of a recursive function, notable especially because it is not a primitive recursive function.
- All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive.
- Its arguments are never negative and it always terminates.
- The two-argument Ackermann–Péter function, is defined as follows:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(m,n) = \begin{cases} n+1 \mbox {if} m=0 \\ A(m-1,1) & \mbox {if} m>0 and n=0 \\ A(m-1,A(m,n-1))& \mbox {if} m>0 and n>0 \end{cases} } \\
for nonnegative integers m and n.
- Its value grows rapidly, even for small inputs.
Example
Related Videos
See Also
References
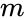 and
and  are the positive integers.
are the positive integers.