Manuals/calci/FTEST
FTEST(ar1,ar2)
- and are array of data.
Description
- This function gives the result of F-test.
- The F-test is designed to test if two population variances are equal.
- It does this by comparing the ratio of two variances.
- So, if the variances are equal, the ratio of the variances will be 1.
- Let X1,...Xn and Y1...Ym be independent samples each have a Normal Distribution .
- It's sample means: and .
- The sample variances :
and
- Failed to parse (syntax error): {\displaystyle SY^2=\frac{1}{m-1} \sum_{i=1}^m (Yi-\bar Y)^2. *Then the Test Statistic = <math>\frac {Sx^2}{Sy^2}<math> has an F-distribution with <math>n−1} and Failed to parse (syntax error): {\displaystyle m − 1} degrees of freedom.
- In FTEST(ar1,ar2) where is the data of first array, is the data of second array.
- The array may be any numbers, names, or references that contains numbers.
- values are not considered if the array contains any text, logical values or empty cells.
When the or is less than 2 or the variance of the array value is zero, then this function will return the result as error.
Examples
1.DATA1 DATA2
15 21 27 12 19 30 32 11
FTEST(B4:B8,C4:C8)=0.81524906747183 2.DATA 1={5,8,12,45,23}; DATA2={10,20,30,40,50}
FTEST(A1:A5,C1:C5)=0.9583035732212274
3. DATA1={14,26,37};DATA2={45,82,21,17} FTEST(B1:B3,C1:C4}=0.26412211240525474 4.DATA1={25},DATA2={45,65} FTEST(B1,C2:C3)=NAN
See Also
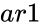 and
and 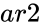 are array of data.
are array of data.