Manuals/calci/FISHER
FISHER(number)
- is the value to find the Fisher transformation.
Description
- This function gives the value of Fisher Transformation for the given number.
- Fisher Transformation is used to test the hypothesis of two correlations.
- It is mainly associated with the Pearson Product-Moment Correlation coefficient for bi-variate normal observations.
- In , is the value which ranges between -1 to +1.
- The transformation is defined by :
where is the natural logarithm function and is the Inverse Hyperbolic function.
- This function will give the result as error when:
1. is non-numeric 2. or .
ZOS Section
- The syntax is to calculate FISHER in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle FISHER(number)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle number} is the value to find the Fisher transformation.
- For e.g.,fisher(0.1..0.4..0.1)
Examples
- FISHER(0.5642) = 0.6389731838284958
- FISHER(0)= 0
- FISHER(-0.3278) = -0.3403614004970268
- FISHER(1) = Infinity
- FISHER(-1) = Infinity
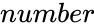 is the value to find the Fisher transformation.
is the value to find the Fisher transformation.