Manuals/calci/REGRESSIONANALYSIS
REGRESSIONANALYSIS (YRange,XRange,ConfidenceLevel,NewTableFlag)
- is the set of dependent variables .
- is the set of independent variables.
- level of Confidence value.
- is either 0 or 1.
- REGRESSIONANALYSIS(), Returns the analysis of numerical data consisting of values of a depeendent and one or more independent variables.
Description
- This function is calculating the Regression analysis of the given data.
- The analysis of numerical data consisting of values of a dependent and one or more independent variables
- This analysis is very useful for the analyzing the large amounts of data and making predictions.
- Regression analysis is a form of predictive modelling technique which investigates the relationship between a dependent and independent variable.
- This technique is used for forecasting, time series modelling and finding the causal effect relationship between the variables.
- This analysis give the result in three table values.
- Regression statistics table.
- ANOVA table.
- Residual output.
1.Regression statistics :
- It contains multiple R, R Square, Adjusted R Square, Standard Error and observations.
- R square gives the fitness of the data with the regression line.
- That value is closer to 1 is the better the regression line fits the data.
- Standard Error refers to the estimated standard deviation of the error term. It is called the standard error of the regression.
2.ANOVA table:
- ANOVA is the analysis of variance.
- This table splits in to two components which is Residual and Regression.
Total sum of squares = Residual (error) sum of squares + Regression (explained) sum of squares.
- Also this table gives the probability, T stat, significance of F and P.
- When the significance of F is < 0.05, then the result for the given data is statistically significant.
- When the significance of F is > 0.05, then better to stop using this set of independent variables.
- Then remove a variable with a high P-value and return the regression until Significance F drops below 0.05.
- So the Significance of P value should be <0.05.
- This table containing the regression coefficient values also.
3.Residual output:
- The residuals show you how far away the actual data points are from the predicted data points.
Examples
1.
| A | B | |
|---|---|---|
| 1 | Temperature | Drying Time(Hrs) |
| 2 | 54 | 8 |
| 3 | 63 | 6 |
| 4 | 75 | 3 |
| 5 | 82 | 1 |
=REGRESSIONANALYSIS(A2:A5,B2:B5,0.65,0)
REGRESSION ANALYSIS OUTPUT
| Regression Statistics | |
|---|---|
| Multiple R | 0.9989241524588297 |
| R Square | 0.9978494623655914 |
| ADJUSTEDRSQUARE | 0.996774193548387 |
| STANDARDERROR | 0.7071067811865526 |
| OBSERVATIONS | 4 |
| DF | SS | MS | F | SIGNIFICANCE F | |
|---|---|---|---|---|---|
| REGRESSION | 1 | 464 | 464 | 927.9999999999868 | 0.001075847541170237 |
| RESIDUAL | 2 | 1.0000000000000142 | 0.5000000000000071 | ||
| TOTAL | 3 | 465 |
| COEFFICIENTS | STANDARD ERROR | T STAT | P-VALUE | LOWER 95% | UPPER 95% | |
|---|---|---|---|---|---|---|
| INTERCEPT | 86.5 | 0.6885767430246896 | 125.62143708199342 | 0.00006336233990811291 | 83.53729339698282 | 89.46270660301718 |
| INDEP1 | -4.000000000000007 | 0.1313064328597235 | -30.46309242345547 | 0.0010758475411701829 | -4.564965981777561 | -3.4350340182224532 |
| OBSERVATION | PREDICTED Y | RESIDUALS | STANDARD RESIDUALS |
|---|---|---|---|
| 1 | 54.49999999999994 | -0.49999999999994316 | -0.8660254037843341 |
| 2 | 62.49999999999996 | 0.5000000000000426 | 0.8660254037845064 |
| 3 | 74.49999999999997 | 0.5000000000000284 | 0.8660254037844818 |
| 4 | 82.5 | -0.5 | -0.8660254037844325 |
Related Videos
See Also
References
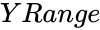 is the set of dependent variables .
is the set of dependent variables .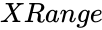 is the set of independent variables.
is the set of independent variables.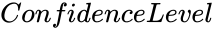 level of Confidence value.
level of Confidence value.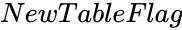 is either 0 or 1.
is either 0 or 1.