Difference between revisions of "Manuals/calci/STDEV"
Jump to navigation
Jump to search
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''STDEV( | + | <div style="font-size:30px">'''STDEV()'''</div><br/> |
| − | * | + | *Parameters are set of numbers. |
| + | **STDEV(), estimates standard deviation based on a sample. | ||
==Description== | ==Description== | ||
| Line 7: | Line 8: | ||
*It is the used as a measure of the dispersion or variation in a distribution. | *It is the used as a measure of the dispersion or variation in a distribution. | ||
*It is calculated as the square root of variance. | *It is calculated as the square root of variance. | ||
| − | *In <math> STDEV( | + | *In <math> STDEV()</math>, Parameters are set of numbers to find the Standard Deviation. |
| − | *Here | + | *Here First parameter is required. From the second parameter are optional. |
*Instead of numbers, we can use the single array or a reference of a array. | *Instead of numbers, we can use the single array or a reference of a array. | ||
*<math> STDEV </math> is defined by the formula: | *<math> STDEV </math> is defined by the formula: | ||
<math>S.D= \sqrt \frac {\sum(x-\bar{x})^2}{(n-1)} </math> | <math>S.D= \sqrt \frac {\sum(x-\bar{x})^2}{(n-1)} </math> | ||
where <math> \bar{x} </math> is the sample mean of <math> x </math> and <math> n </math> is the total numbers of the given data. | where <math> \bar{x} </math> is the sample mean of <math> x </math> and <math> n </math> is the total numbers of the given data. | ||
| − | *It is calculated using <math> | + | *It is calculated using <math>n-1</math> method. |
*This function is considering our given data is the sample of the population. | *This function is considering our given data is the sample of the population. | ||
*Suppose it should consider the data as the entire population, we can use the [[Manuals/calci/STDEVP | STDEVP ]] function. | *Suppose it should consider the data as the entire population, we can use the [[Manuals/calci/STDEVP | STDEVP ]] function. | ||
Latest revision as of 17:17, 8 August 2018
STDEV()
- Parameters are set of numbers.
- STDEV(), estimates standard deviation based on a sample.
Description
- This function gives the Standard Deviation based on a given sample.
- Standard Deviation is the quantity expressed by, how many members of a group differ from the mean value of the group.
- It is the used as a measure of the dispersion or variation in a distribution.
- It is calculated as the square root of variance.
- In , Parameters are set of numbers to find the Standard Deviation.
- Here First parameter is required. From the second parameter are optional.
- Instead of numbers, we can use the single array or a reference of a array.
- is defined by the formula:
where is the sample mean of and is the total numbers of the given data.
- It is calculated using method.
- This function is considering our given data is the sample of the population.
- Suppose it should consider the data as the entire population, we can use the STDEVP function.
- The arguments can be be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text,logical values or empty cells, like that values are not considered.
- When we are entering logical values and text representations of numbers as directly, then the arguments are counted.
- Suppose the function have to consider the logical values and text representations of numbers in a reference , we can use the STDEVA function.
- This function will return the result as error when
1. Any one of the argument is non-numeric.
2. The arguments containing the error values or text that cannot be translated in to numbers.
Examples
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 0 | 4 | 6 | 10 | 12 | 15 |
| 2 | 7 | 3 | -1 | 2 | 25 | |
| 3 | 9 | 11 | 8 | 6 | 15 |
- =STDEV(18,25,76,91,107) = 39.8660256358
- =STDEV(208,428,511,634,116,589,907) = 267.0566196431
- =STDEV(A1:F1) = 5.52871293039
- =STDEV(A2:D2) = 3.304037933599
- =STDEV(A3:B3) = 1.414213562373
- =STDEV(12,18,27,32,FALSE) = 12.617448236470002
Related Videos
See Also
References
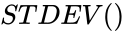 , Parameters are set of numbers to find the Standard Deviation.
, Parameters are set of numbers to find the Standard Deviation.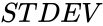 is defined by the formula:
is defined by the formula: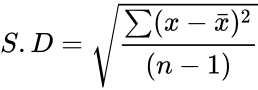
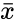 is the sample mean of
is the sample mean of  and
and  is the total numbers of the given data.
is the total numbers of the given data.
 method.
method.