Manuals/calci/COMBINATIONS
Jump to navigation
Jump to search
COMBINATIONS (Array,HowMany)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array } is the set of numbers.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle HowMany} is the number of choices.
Description
- This function shows the combination of the given numbers.
- A combination is a selection of all or part of a set of objects, without regard to the order in which objects are selected.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle COMBINATIONS (Array,HowMany)} , is the set of numbers and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Howmany} is the described number of choice.
- The number of ways of picking k unordered outcomes from n possibilities.
- Also known as the binomial coefficient or choice number and read "n choose k" .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle _nC_k =\binom{n}{k}= \frac{n!}{k!(n-k)!}} .
- Here COMBINATIONS shows the choices of the selected objects.
Examples
1.COMBINATIONS([3,8,12],2)
| 3 | 8 |
| 3 | 12 |
| 8 | 12 |
2.COMBINATIONS([10,18,300,23,192],3)
| 10 | 18 | 300 |
| 10 | 18 | 23 |
| 10 | 18 | 192 |
| 10 | 300 | 23 |
| 10 | 300 | 192 |
| 10 | 23 | 192 |
| 18 | 300 | 23 |
| 18 | 300 | 192 |
| 18 | 23 | 192 |
| 300 | 23 | 192 |
Related Videos
See Also
References
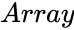 is the set of numbers and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Howmany}
is the described number of choice.
is the set of numbers and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Howmany}
is the described number of choice.