Manuals/calci/COTH
Jump to navigation
Jump to search
COTH(x)
- where x is any real number.
- COTH() returns the inverse hyperbolic tangent of a number.
Description
- This function gives the hyperbolic Cotangent of 'x'.
- It's also called as Circular function.
- Let z is any real number.
- COTH is the reciprocal of TANH function.i.e.COTH(z)=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (tanh (z))^{-1}}
- i.e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {e^z+e^{-z}} {e^z-e^{-z}}} or iCOT(iz).where 'i' is the imaginary unit and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=\sqrt{-1}} .
- Also relation between Hyperbolic & Trignometric function is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cot(iz)=-iCoth(z)} & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Coth(iz)=-iCot(z)}
Examples
COTH(x)
- x is any real number.
| COTH(x) | Value |
| COTH(1) | 1.3130352854993312 |
| COTH(30) | 1 |
| COTH(-45) | -1 |
Related Videos
See Also
References
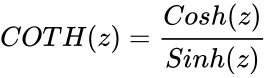 i.e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {e^z+e^{-z}} {e^z-e^{-z}}}
or iCOT(iz).where 'i' is the imaginary unit and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=\sqrt{-1}}
.
i.e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {e^z+e^{-z}} {e^z-e^{-z}}}
or iCOT(iz).where 'i' is the imaginary unit and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=\sqrt{-1}}
.