Manuals/calci/EIGENVALUES
Jump to navigation
Jump to search
EIGENVALUES (Matrix)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Matrix} is the array of numeric elements.
Description
- This function shows the Eigen value of the given matrix.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle EIGENVALUES (Matrix)} , is any matrix values.
- In linear algebra, an eigen vector or characteristic vector of a linear transformation is a non-zero vector whose direction does not change when that linear transformation is applied to it.
- Let A be a linear transformation represented by a matrix A.
- Let A is an nxn matrix, v is a non zero nx1 vector and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} is a scalar which may be either real or complex.
- Any value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} for which this equation has a solution is known as an eigenvalue of the matrix A.
- It is sometimes also called the characteristic value.
- The vector, v, which corresponds to this value is called an eigenvector.
- The eigenvalue problem can be rewritten as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (A-\lambda.I).v=0} .
- If v is non-zero, this equation will only have a solution if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |A-\lambda.I|.v=0} .
- This equation is called the characteristic equation of A, and is an nth order polynomial in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} with n roots.
- These roots are called the eigenvalues of A.
Examples
| A | B | C | |
|---|---|---|---|
| 1 | 3 | 7 | 5 |
| 2 | 10 | 12 | 8 |
| 3 | 6 | 8 | 14 |
=EIGENVALUES(A1:C3)
-2.018987498930866 |
25.303239119591886 |
5.715748379338994 |
-0.8195524172935329 0.3557792393359474 0.2128903683040517 |
0.5726193656991498 0.663334322125492 0.6212592923173481 |
0.02099755544415341 0.6583378387635402 -0.7541316747045657 |
| A | B | |
|---|---|---|
| 1 | 5 | 6 |
| 2 | 9 | -11 |
=EIGENVALUES(A1:B2)
-13.862780491200214 |
7.8627804912002155 |
0.3031213645114406 0.9025310769284506 |
-0.9529519601620652 0.43062472662211493 |
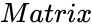 is any matrix values.
is any matrix values.