Manuals/calci/HESSENBERG
MATRIX("HESSENBERG",order)
- is the order of the Hessenberg matrix.
Description
- This function gives the matrix with the property of Hessenberg matrix.
- A Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular.
- To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal.
- Here MATRIX("hessenberg") displays the hessenberg matrix of order 3.
- An nxn matrix with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{i,j}=0} for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i> j+1} is called a Hessenberg matrix.
- So the form of a Hessenberg matrix is: \begin{bmatrix}
a_{11} & a_{12} & a_{13} \cdots & a_{1(n-1)}& a_{1n} \\ a_{21} & a_{22} & a_{23} \cdots& a_{2(n-1)}& a_{2n} \\ 0 & a_{32} & a_{33} \cdots& a_{3(n-1)}& a_{3n} \\ 0 & 0 & a_{43} \cdots& a_{4(n-1)}& a_{4n} \\ 0 & 0 & 0 \cdots& a_{5(n-1)}& a_{5n} \\ \vdots & \ddots & \vdots \\ 0 & 0 & 0 & a_{(n-1)(n-2)} & a_{(n-1)(n-1)} & a_{(n-1)n}\\ 0 & 0 & 0 & 0 & a_{n(n-1)} & a_{nn}\\ \end{bmatrix}
- So the matrix is zero below the first subdiagonal.
- If the matrix is symmetric or Hermitian, the form is tridiagonal.
Examples
- 1.MATRIX("hessenberg") =53
- 2.MATRIX("hessenberg",3)
| -10 | -50 | -92 |
| -32 | 62 | 33 |
| 0 | -99 | -81 |
- 3.MATRIX("hessenberg",6)
| 99 | 88 | -73 | 20 | -17 | -10 |
| -28 | 40 | -2 | 15 | -48 | 55 |
| 0 | -46 | 56 | -76 | -85 | -70 |
| 0 | 0 | 12 | -72 | 72 | -17 |
| 0 | 0 | 0 | -67 | -26 | -6 |
| 0 | 0 | 0 | 0 | -13 | 50 |
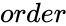 is the order of the Hessenberg matrix.
is the order of the Hessenberg matrix.