KSTESTNORMAL (XRange,ObservedFrequency,Confidence,DoMidPointOfIntervals,NewTableFlag)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle XRange}
is the array of x values.
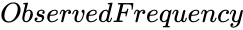 is the frequency of values to test.
is the frequency of values to test.- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Confidence}
is the mean Value.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle DoMidPointOfIntervals}
is the standard deviation of the set of values.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NewTableFlag}
is either TRUE or FALSE.
Description
- This function gives the test statistic of the K-S test.
- K-S test is indicating the Kolmogorov-Smirnov test.
- It is one of the non parametric test.
- This test is the equality of continuous one dimensional probability distribution.
- It can be used to compare sample with a reference probability distribution or to compare two samples.
- This test statistic measures a distance between the empirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples.
- The two-sample KS test is one of the most useful and general nonparametric methods for comparing two samples.
- It is sensitive to differences in both location and shape of the empirical cumulative distribution functions of the two samples.
- This test can be modified to serve as a goodness of fit test.
- The assumption of the KS test is:
- Null Hypothesis(H0):The sampled population is normally distributed.
- Alternative hypothesis(Ha):The sampled population is not normally distributed.
- The Kolmogorov-Smirnov test to compare a data set to a given theoretical distribution is as follows:
- 1.Data set sorted into increasing order and denoted as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i}
, where i=1,...,n.
- 2.Smallest empirical estimate of fraction of points falling below Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i}
, and computed as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{(i-1)}{n}}
for i=1,...,n.
- 3.Largest empirical estimate of fraction of points falling below Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i}
and computed as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{i}{n}}
for i=1,...,n.
- 4.Theoretical estimate of fraction of points falling below Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i}
and computed as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x_i)}
, where F(x) is the theoretical distribution function being tested.
- 5.Find the absolute value of difference of Smallest and largest empirical value with the theoretical estimation of points.
- This is a measure of "error" for this data point.
- 6.From the largest error, we can compute the test statistic.
- The Kolmogorov-Smirnov test statistic for the cumulative distribution F(x) is:Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_n=Sup_x|F_n(x)-F(x)|}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sup_x}
is the supremum of the set of distances.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_n(x)}
is the empirical distribution function for n,with the observations Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_i}
is defined as:Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_n(x)=\frac{1}{n}\sum_{i=1}^n I_{X_i\le x}}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{X_i\le x}}
is the indicator function, equal to 1 if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_i\le x}
and equal to 0 otherwise.
Example
Spreadsheet
|
A |
B
|
| 1
|
15 |
20
|
| 2
|
17 |
14
|
| 3
|
19 |
16
|
| 4
|
21 |
25
|
| 5
|
23 |
27
|
- =KSTESTNORMAL(A1:A5,B1:B5,19,3.16)
KOLMOGOROV-SMIRNOV TEST
| DATA |
OBSERVED FREQUENCY |
CUMULATIVE OBSERVED FREQUENCY |
SN |
Z-SCORE |
F(X) |
DIFFERENCE
|
| 15 |
20 |
20 |
0.19608 |
-0.74915 |
0.22688 |
0.03081
|
| 17 |
14 |
34 |
0.33333 |
-0.07293 |
0.47093 |
0.1376
|
| 19 |
16 |
50 |
0.4902 |
0.6033 |
0.72684 |
0.23665
|
| 21 |
25 |
75 |
0.73529 |
1.27952 |
0.89964 |
0.16435
|
| 23 |
27 |
102 |
1 |
1.95574 |
0.97475 |
0.02525
|
TEST STATISTICS
| ANALYSIS
|
| MEAN |
17.21569
|
| STANDARDDEVIATION |
2.95761
|
| COUNT |
5
|
| D |
0.23665
|
| D-CRITICAL |
#ERROR
|
KS TEST
TYPE NORMALDIST
- CONCLUSION - THE DATA IS NOT A GOOD FIT WITH THE DISTRIBUTION.
Related Videos
See Also
References
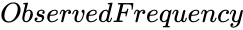 is the frequency of values to test.
is the frequency of values to test.