Manuals/calci/MANDELBROT
Jump to navigation
Jump to search
MANDELBROT (SettingsArray,Width,Height,MandeliterFunction,Shades,CanvasId)
Description
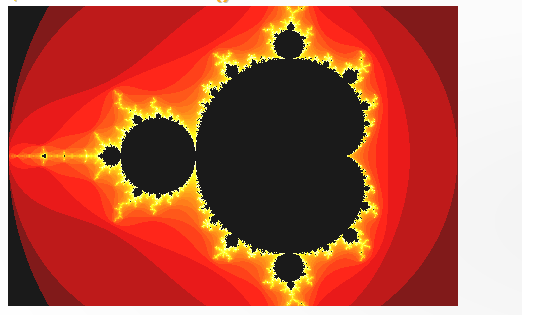
- This function shows the figure of the Mandelbrot.
- Fractals are infinitely complex patterns that are self-similar across different scales.
- This property is called self-similarity.
- Fractals form a never ending pattern, created by repeating a simple process over and over, in an ongoing feedback loop.Mandelbrot Set is the set of points in the complex plane with the sequence where the result does not approach infinity.
- The Julia Set is closely related to Mandelbrot Set.
- The Mandelbrot Set is obtained from the quadratic recurrence equation , (with=0), where points c in the complex plane for which the computed value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_n} does not tend to infinity.
Examples
- MANDELBROT()
Related Videos
See Also
References
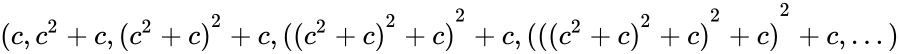 where the result does not approach infinity.
where the result does not approach infinity.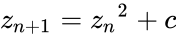 , (with
, (with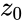 =0), where points c in the complex plane for which the computed value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_n}
does not tend to infinity.
=0), where points c in the complex plane for which the computed value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_n}
does not tend to infinity.