Manuals/calci/MATRIXINVERSE
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is any matrix.
Description
- This function shows the inverse value of the given matrix.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MATRIXINVERSE (a)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is any square matrix.
- Inverse of a square matrix is also called reciprocal of a matrix and it is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{-1}} .
- Consider the square matrix A has an inverse which should satisfies the following condition Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |A|\ne 0}
- Also Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AA^{-1}=I} (Identity matrix).
- Consider 2x2 matrix:A=[a b;c d].
- The inverse of matrix A is calculated by
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{-1}={\begin{bmatrix} a & b \\ c & d \end{bmatrix}}^{-1}} = =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}}
- Consider 3x3 matrix A and its inverse is calculated by
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{-1}={\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}}^{-1}} =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{det A }{\begin{bmatrix} A & B & C \\ D & E & F \\ G & H & I \end{bmatrix}}^T } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{det A } {\begin{bmatrix} A & D & G \\ B & E & H \\ C & F & I \end{bmatrix}}}
where A=(ei-fh); B=-(di-fg);C=(dh-eg); D=-(bi-ch); E=(ai-cg); F=-(ah-bg); G=(bf-ce) H=-(af-cd);I=(ae-bd)
Examples
1. MATRIXINVERSE([4,7;2,6])
| 0.6 | -0.7 |
| -0.2 | 0.4 |
2. MATRIXINVERSE([1,2,3;0,1,4;5,6,0])
| -24 | 18 | 5 |
| 20 | -15 | -4 |
| -5 | 4 | 1 |
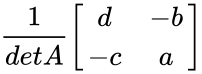 =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}}
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}}