Manuals/calci/MATRIXPLUS
Jump to navigation
Jump to search
MATRIXPLUS (a,b,ConsiderUnits)
- and are any two matrices.
Description
- This function calculates the addition of the two matrices.
- In , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} are two matrices.
- Matrix addition is the basic operation of adding two matrices with the corresponding entries.
- Two matrices must have an equal number of rows and columns.
- The sum of matrices A and B is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A+B= \begin{bmatrix} a_{11} & a_{12}&\cdots & a_{1n} \\ a_{21}& a_{22}& \cdots & a_{2n} \\ \vdots & \ddots & \vdots \\ a_{m1} & a_{m2}& \cdots & a_{mn} \end{bmatrix} +\begin{bmatrix} b_{11} & b_{12}&\cdots & b_{1n} \\ b_{21}& b_{22}& \cdots & b_{2n} \\ \vdots & \ddots & \vdots \\ b_{m1} & b_{m2}& \cdots & b_{mn} \end{bmatrix} = \begin{bmatrix} a_{11}+b_{11} & a_{12}+b_{12}&\cdots & a_{1n}+b_{1n} \\ a_{21}+b_{21}& a_{22}+b_{22}& \cdots & a_{2n}+b_{2n} \\ \vdots & \ddots & \vdots \\ a_{m1}+b_{m1} & a_{m2}+b_{m2}& \cdots & a_{mn}+b_{mn} \end{bmatrix}}
Examples
1. MATRIXPLUS([2,3,4;5,6,7],[9,12,43;20,26,87])
| 11 | 15 | 47 |
| 25 | 32 | 94 |
2. MATRIXPLUS([-45,30.4;12,65;98,-44],[92,34;-87,26;77,56])
| 47 | 64.4 |
| -75 | 91 |
| 175 | 12 |
Related Videos
See Also
References
 and
and 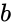 are any two matrices.
are any two matrices.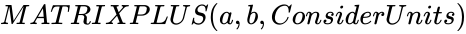 ,
,