Manuals/calci/REMAINDER
Jump to navigation
Jump to search
REMAINDER(Number,Divisor)
OR
MOD (Number,Divisor)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number} is a single number or set of numbers, and
- is any real number.
- REMAINDER(),returns the remainder from division.
Description
- This function gives the remainder of the number after dividing with given number. This is similar to function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MOD()}
- When we divide two integers we will get the result like this: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{X}{Y}= Q} with remainder Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} . Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X } is the dividend, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} is the divisor, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} is the Quotient and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} is the remainder.So Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle REMAINDER(X,Y)=R} .
- This function will return the result as error when the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} value is 0.
- Suppose the value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} with same sign either '+' or '-',then the result is also displayed with the same sign.
- But if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} are with different signs,one positive and other negative, then the result will have Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} sign only.
ZOS
- The syntax is to calculate remainder of the given numbers in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle REMAINDER(Number,Divisor)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Divisor} are any real numbers.
- For e.g.,REMAINDER(10,2),REMAINDER(50.2,-4)
Examples
- =REMAINDER(7,2)=1
- =REMAINDER(-11,-3)=-2
- =REMAINDER(75,5)=0
- =REMAINDER(12,-4)=0
- =REMAINDER(85,-9)=-5
- =REMAINDER(-52,7)=4
- =REMAINDER(0,9)=0
- =REMAINDER(9,0)=#N/A (DIVISOR == 0)
- =REMAINDER(5.5,2)=1.5
For an array of numbers/dividends, a table with remainder values is displayed as follows -
- REMAINDER(11..15,4)
| Number | Divisor | MOD |
|---|---|---|
| 11 | 4 | 3 |
| 12 | 4 | 0 |
| 13 | 4 | 1 |
| 14 | 4 | 2 |
| 15 | 4 | 3 |
- REMAINDER([66,34,21],8)
| Number | Divisor | MOD |
|---|---|---|
| 66 | 8 | 2 |
| 34 | 8 | 2 |
| 21 | 8 | 5 |
Related Videos
See Also
References
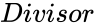 is any real number.
is any real number.