Manuals/calci/SIGNTEST
Jump to navigation
Jump to search
SIGNTEST(Array,Median,AlternateHypothesis,NewTableFlag)
- is the set of values to find the statistic value.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Median} is the median of the array of values.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AlternateHypothesis} is the alternate hypothesis of the array.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NewTableFlag} is either TRUE or FALSE.
Description
- This function gives the test statistic of the Sign test.
- The Sign Test is ued to test the Hypothesis that there is no difference between two continuous distributions X and Y.
- This test is one type of the Non parametric Test.
- The sign test is designed to test a hypothesis about the location of a population distribution.
- The Sign test does not require the assumption that the population is normally distributed.
- The normality of the distribution is doubtable, then Sign test is used to find the statitic instead of one sample T-test.
- The sign test uses the sign of the differences, unlike the paired t test which uses the sign and magnitude of the differences.
- To perform this test, Consider the independent pairs of sample data from the populations Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {(x_1,y_1)(x_2,y_2).....(x_n,y_n)}} .
- From this pair,it must be omitted with no differences Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_i=y_i)} .
- The Sign test data are having the following properties:
- 1.The differences of pairs are assumed to be independent.
- 2.Each pairs comes from the same continuous population.
- 3.The values Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_i} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_i} represent are ordered , so the comparisons "greater than", "less than", and "equal to" are meaningful.
- The test statistic is expected to follow a binomial distribution, the standard binomial test is used to calculate significance.
- The sign test can also be viewed as testing the hypothesis that the median of the differences is zero.
- The sign test Hypothesis is having the following steps:
- Step1:State Null and Alternative Hypothesis
- Two ways to state these: One sample or sample of differences, want to test specific value for the population median M.
- Null: H0:p=1/2is equivalent to M = M0.
- Alternative: Ha:p<1/2 is equivalent to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M>M_0} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ha: p>1/2} is equivalent to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M < M_0} or Ha:p not equal to 1/2 is equivalent to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\ne M_0}
- Step2:Test statistic (no data conditions needed)
- S+ = Number of observations greater than Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_0} or Number of observations with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x>y} .
- S− = Number of observations less than Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_0} or Number of observations with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x<y} .
- Ties are not used, so use n = S+ + S−.
- Step3: Finding the p-value
- Remember, p-value is:
- Probability of observing a test statistic as large as or larger than that observed
- in the direction that supports Ha
- if the null hypothesis is true.
- Step 4:Use tables of the binomial distribution to find the probability of observing a value of
r or higher assuming p = 1/2 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = n_0} .
- If the test is one-sided, this is your p-value.
- Step5: If the test is a two-sided test, double the probability to obtain the p-value.
Example
| A | B | |
|---|---|---|
| 1 | 15 | 10 |
| 2 | 19 | 17 |
| 3 | 32 | 35 |
| 4 | 42 | 38 |
| 5 | 24 | 16 |
- =SIGNTEST(A1:B5,5,10,true)
| X Range | Y Range | Difference |
|---|---|---|
| 15 | 10 | 5 |
| 19 | 17 | 2 |
| 32 | 35 | -3 |
| 42 | 38 | 4 |
| 24 | 16 | 8 |
| P-Value | 0.375 |
Related Videos
See Also
References
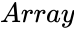 is the set of values to find the statistic value.
is the set of values to find the statistic value.