Manuals/calci/SINCP
Jump to navigation
Jump to search
SINCP(X)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} is any real number.
Description
- This function shows the value of the cardinal normalized sin function.
- In , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} is any real number.
- The full name of the function is normalized sine cardinal,but it is commonly referred to by its abbreviation, Sincp.
- The unnormalized SINC function is defined by :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SINC(X)=\begin{cases} 1 & for x=0 \\ \frac{Sin x}{x} & Otherwise\\ \end{cases}}
- The normalized SINC function is called as SINCP and it is defined by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SINCP(X)= SINC(PI()*X)} .
- The value at x = 0 is defined to be the limiting value Sinc(0) = 1.
- The only difference between the two definitions is in the scaling of the independent variable (the x-axis) by a factor of π.
Examples
- SINCP(23) = 8.814971340095828e-17
- SINCP(-12) = -3.8981718325193755e-17
- SINCP(45.3) = -0.0056847264326763776
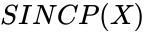 , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X}
is any real number.
, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X}
is any real number.