Manuals/calci/TENSORPRODUCT
OR
- and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} are any two matrices.
Description
- This function shows the Tensor product of the matrix.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle TENSORPRODUCT (a,b)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} are any two matrices.
- Here matrices Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} should be square matrix with same order.
- Tensor product is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \otimes} .
- Tensor product is different from general product.
- The Tensor product is defined by the product two vector spaces V and W is itself a Vector space.
- It is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\otimes W} .
- A DYADIC product is the special case of the tensor product between two vectors of the same dimension.
- The tensor product of V and W is the vector space generated by the symbols Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v\otimes w } , with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v \isin V} and .
- The tensor product from the direct sum vector space, whose dimension is the sum of the dimensions of the two summands:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dim (V \otimes W)= dim V +dim W }
- Now consider any 2x2 matrices:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}\otimes \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} = \begin{bmatrix} a_{11}\begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} a_{12} \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} \\ a_{21} \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} a_{22} \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} \end{bmatrix} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} a_{11}b_{11} & a_{11}b_{12} & a_{12}b_{11} & a_{12}b_{12}\\ a_{11}b_{21} & a_{11}b_{22} & a_{12}b_{21} & a_{12}b_{22}\\ a_{21}b_{11} & a_{21}b_{12} & a_{22}b_{11} & a_{22}b_{12}\\ a_{21}b_{21} & a_{21}b_{22} & a_{22}b_{21} & a_{22}b_{22} \end{bmatrix} }
Examples
1. TENSORPRODUCT([[2,3],[1,0]],[[10,2],[6,-18]])
| 20 | 4 | 30 | 6 |
| 12 | -36 | 18 | -54 |
| 10 | 2 | 0 | 0 |
| 6 | -18 | 0 | 0 |
2. TENSORPRODUCT([[3,7.3,6],[10,11,-6],[8,5,3]],[[12,4,-5],[6,10,3],[3.5,9,5.4]])
| 36 | 12 | -15 | 87.6 | 29.2 | -36.5 | 72 | 24 | -30 |
| 18 | 30 | 9 | 43.8 | 73 | 21.9 | 36 | 60 | 18 |
| 10.5 | 27 | 16.200000000000003 | 25.55 | 65.7 | 39.42 | 21 | 54 | 32.400000000000006 |
| 120 | 40 | -50 | 132 | 44 | -55 | -72 | -24 | 30 |
| 60 | 100 | 30 | 66 | 110 | 33 | -36 | -60 | -18 |
| 35 | 90 | 54 | 38.5 | 99 | 59.400000000000006 | -21 | -54 | -32.400000000000006 |
| 96 | 32 | -40 | 60 | 20 | -25 | 36 | 12 | -15 |
| 48 | 80 | 24 | 30 | 50 | 15 | 18 | 30 | 9 |
| 28 | 72 | 43.2 | 17.5 | 45 | 27 | 10.5 | 27 | 16.200000000000003 |
3.TENSORPRODUCT(1,2,3,4,5,6).print()
[ [4,5,6,8,10,12,12,15,18 ] ]
4. TENSORPRODUCT([[1],[2],[3]],[[4],[5],[6]]).print()
[ [4 ],
[5 ],
[6 ],
[8 ],
[10 ],
[12 ],
[12 ],
[15 ],
[18 ] ]
5. TENSORPRODUCT([[1],[2],[3]],[[4],[5]]).print()
[ [4 ],
[5 ],
[8 ],
[10 ],
[12 ],
[15 ] ]
 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b}
are any two matrices.
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b}
are any two matrices.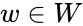 .
.