Manuals/calci/TORUS
Jump to navigation
Jump to search
TORUS (Radius,TubeRadius,w1)
where
- and are radius value of the circle.
- TORUS() shows the Torus for the given value.
Description
TORUS (Radius,TubeRadius,w1)
- is the radius value of the bigger circle.
- is the radius value of the smaller circle.
- A torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis co planar with the circle. *If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution.
- For example of TORUS are rings, doughnuts, and bagels.
- A torus can be defined parametrically by:
where , are angles which make a full circle, so that their values start and end at the same point.
- is the distance from the center of the tube to the center of the torus.
- is the radius of the tube.
- is known as the "major radius" and is known as the "minor radius".
- The ratio R divided by r is known as the aspect ratio.
- The typical doughnut confectionery has an aspect ratio of about 3 to 2.
Examples
Related Videos
See Also
References
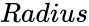 and
and 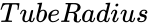 are radius value of the circle.
are radius value of the circle.
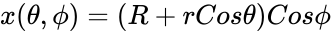
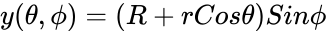
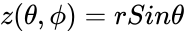
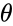 ,
,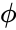 are angles which make a full circle, so that their values start and end at the same point.
are angles which make a full circle, so that their values start and end at the same point.
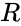 is the distance from the center of the tube to the center of the torus.
is the distance from the center of the tube to the center of the torus.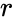 is the radius of the tube.
is the radius of the tube.