Difference between revisions of "Manuals/calci/BESSELK"
Jump to navigation
Jump to search
| Line 9: | Line 9: | ||
*But in most of the cases α is the non-negative real number. | *But in most of the cases α is the non-negative real number. | ||
*The solutions of this equation are called Bessel Functions of order n. Bessel functions of the first kind, denoted as Jn(x), and | *The solutions of this equation are called Bessel Functions of order n. Bessel functions of the first kind, denoted as Jn(x), and | ||
| − | *The Bessel function of the first kind of order can be expressed as:Jn(x)=summation(k=0 to infinity){(-1)^k(x/2)^n+2k}/k!gamma(n+k+1 | + | *The Bessel function of the first kind of order can be expressed as:<math>Jn(x)=summation(k=0 to infinity){(-1)^k(x/2)^n+2k}/k!gamma(n+k+1</math>. |
*The Bessel function of the second kind Yn(x).The Bessel function of the 2nd kind of order can be expressed as: Yn(x)=lt p tends to n {Jp(x)Cosp pi()- J-p(x)}/Sinp pi(). | *The Bessel function of the second kind Yn(x).The Bessel function of the 2nd kind of order can be expressed as: Yn(x)=lt p tends to n {Jp(x)Cosp pi()- J-p(x)}/Sinp pi(). | ||
*So the form of the general solution is y(x)=c1 In(x)+c2 Kn(x). where In(x)=i^-nJn(ix) and Kn(x)=lt p tends to n pi()/2[( I-p(x)-I p(x))/Sinp pi()] are the modified Bessel functions of the first and second kind respectively.This function will give the result as error when 1.x or n is non numeric | *So the form of the general solution is y(x)=c1 In(x)+c2 Kn(x). where In(x)=i^-nJn(ix) and Kn(x)=lt p tends to n pi()/2[( I-p(x)-I p(x))/Sinp pi()] are the modified Bessel functions of the first and second kind respectively.This function will give the result as error when 1.x or n is non numeric | ||
Revision as of 00:26, 2 December 2013
BESSELK(x,n)
- Where is the value at which to evaluate the function
- is the integer which is the order of the Bessel Function
Description
- This function gives the value of the modified Bessel function when the arguments are purely imaginary.
- Bessel functions is also called cylinder functions because they appear in the solution to Laplace's equation in cylindrical coordinates.
- Bessel's Differential Equation is defined as:Failed to parse (syntax error): {\displaystyle x^2 (d^2 y/dx^2) + x(dy/dx) + (x^2 - α^2)y =0}
where α is the arbitary complex number.
- But in most of the cases α is the non-negative real number.
- The solutions of this equation are called Bessel Functions of order n. Bessel functions of the first kind, denoted as Jn(x), and
*The Bessel function of the first kind of order can be expressed as:.
- The Bessel function of the second kind Yn(x).The Bessel function of the 2nd kind of order can be expressed as: Yn(x)=lt p tends to n {Jp(x)Cosp pi()- J-p(x)}/Sinp pi().
- So the form of the general solution is y(x)=c1 In(x)+c2 Kn(x). where In(x)=i^-nJn(ix) and Kn(x)=lt p tends to n pi()/2[( I-p(x)-I p(x))/Sinp pi()] are the modified Bessel functions of the first and second kind respectively.This function will give the result as error when 1.x or n is non numeric
2. n<0, because n is the order of the function.
Examples
- BESSELK(5,2)=0.005308944 (EXCEL)Kn(x) =0.0040446134(CALCI)K1(x)
- BESSELK(0.2,4)=29900.2492 (EXCEL)Kn(x)=4.7759725484(CALCI)K1(x)
- BESSELK(10,1)=0.000155369
- BESSELK(2,-1)=NAN
 is the value at which to evaluate the function
is the value at which to evaluate the function is the integer which is the order of the Bessel Function
is the integer which is the order of the Bessel Function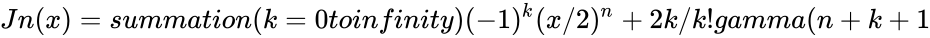 .
.