Difference between revisions of "Manuals/calci/GAMMAINV"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''GAMMAINV(prob,alpha,beta)'''</div><br/> | <div style="font-size:30px">'''GAMMAINV(prob,alpha,beta)'''</div><br/> | ||
| − | * | + | *<math>prob</math> is the probability value associated with gamma distribution |
| − | * | + | *<math>alpha</math>& <math>beta</math> are the values of the shape and rate parameters |
==Description== | ==Description== | ||
| − | *This function gives the inverse value of | + | *This function gives the inverse value of Cumulative Gamma Probability Distribution. |
| − | *This distribution is the | + | *This distribution is the Continuous Probability Distribution on the positive real line and it is of the reciprocal of a variable distributed according to the gamma distribution with two parameters <math>\alpha</math> & <math>\beta</math>. |
*It is used in Bayesian statistics. | *It is used in Bayesian statistics. | ||
| − | *In <math>GAMMAINV(prob,alpha,beta)</math> , prob is the probability value associated with | + | *In <math>GAMMAINV(prob,\alpha,\beta)</math> , <math>prob</math> is the probability value associated with Gamma Distribution,<math>\alpha</math> is called shape parameter and <math>beta</math> is the rate parameter of the distribution. |
| − | * | + | *If <math>GAMMADIST(x,alpha,beta,TRUE)=prob</math>, then <math>GAMMAINV(prob,alpha,beta,)= x</math>. |
| − | *GAMMAINV | + | *GAMMAINV use the iterating method to find the value of <math>x</math>. |
| + | *Suppose the iteration has not converged after 100 searches, then the function gives the error result. | ||
*This function will give the error result when | *This function will give the error result when | ||
| − | + | 1.Any one of the arguments are non-numeric | |
| − | + | 2.<math>\alpha \le 0 </math> or <math>\beta \le 0 </math> | |
| − | + | 3.<math>prob < 0</math> or <math> prob > 1 </math> | |
==Examples== | ==Examples== | ||
| − | #GAMMAINV(0.65189,2,5)=11.1335534510 | + | #=GAMMAINV(0.65189,2,5) = 11.1335534510 |
| − | #GAMMAINV(0.006867292,5,7)=8. | + | #=GAMMAINV(0.006867292,5,7) = 8.155481331 |
| − | #GAMMAINV(1,9,3)=82.51739521528073 | + | #=GAMMAINV(0.1543869,9,3) = 18.0467153645 |
| − | #GAMMAINV(1.1,9,3)=NAN, because prob>1 | + | #=GAMMAINV(1,9,3) = 82.51739521528073 |
| + | #=GAMMAINV(1.1,9,3) = NAN, because <math> prob>1 </math> | ||
| + | |||
==See Also== | ==See Also== | ||
*[[Manuals/calci/GAMMADIST | GAMMADIST]] | *[[Manuals/calci/GAMMADIST | GAMMADIST]] | ||
Revision as of 04:27, 4 December 2013
GAMMAINV(prob,alpha,beta)
- is the probability value associated with gamma distribution
- & are the values of the shape and rate parameters
Description
- This function gives the inverse value of Cumulative Gamma Probability Distribution.
- This distribution is the Continuous Probability Distribution on the positive real line and it is of the reciprocal of a variable distributed according to the gamma distribution with two parameters & .
- It is used in Bayesian statistics.
- In , is the probability value associated with Gamma Distribution, is called shape parameter and is the rate parameter of the distribution.
- If , then .
- GAMMAINV use the iterating method to find the value of .
- Suppose the iteration has not converged after 100 searches, then the function gives the error result.
- This function will give the error result when
1.Any one of the arguments are non-numeric 2. or 3. or
Examples
- =GAMMAINV(0.65189,2,5) = 11.1335534510
- =GAMMAINV(0.006867292,5,7) = 8.155481331
- =GAMMAINV(0.1543869,9,3) = 18.0467153645
- =GAMMAINV(1,9,3) = 82.51739521528073
- =GAMMAINV(1.1,9,3) = NAN, because
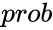 is the probability value associated with gamma distribution
is the probability value associated with gamma distribution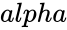 &
&  are the values of the shape and rate parameters
are the values of the shape and rate parameters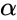 &
& 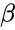 .
.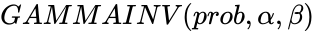 ,
, 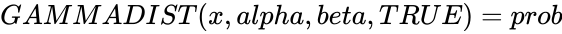 , then
, then 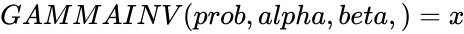 .
. .
.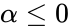 or
or 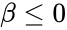 3.
3.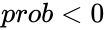 or
or