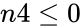Difference between revisions of "Manuals/calci/HYPGEOMDIST"
Jump to navigation
Jump to search
| Line 18: | Line 18: | ||
3.Each individual can be success (S) or a failure (F), | 3.Each individual can be success (S) or a failure (F), | ||
and there are M successes in the population. | and there are M successes in the population. | ||
| − | 4.A sample of n individuals is selected without replacement in such a way that each subset of size n is equally likely to be chosen. The Hyper geometric probability distribution is: | + | 4.A sample of n individuals is selected without replacement in such a way that each subset of size n is equally likely to be chosen. |
| + | *The Hyper geometric probability distribution is: | ||
<math>\frac{\binom{m}{x} \binom{N-M}{n-x}}{\binom{m}{x}}</math> | <math>\frac{\binom{m}{x} \binom{N-M}{n-x}}{\binom{m}{x}}</math> | ||
for <math>x</math> is an integer satisfying <math>max(0, n-N+M)<=x<=min(n,M)</math>. where <math>x</math> is sample's success. | for <math>x</math> is an integer satisfying <math>max(0, n-N+M)<=x<=min(n,M)</math>. where <math>x</math> is sample's success. | ||
Revision as of 05:44, 10 December 2013
HYPGEOMDIST(n1,n2,n3,n4)
- is the sample's success.
- is the sample's size.
- is population's success.
- is the population size.
Description
- This function gives the result of Hypergeometric Distribution.
- This distribution is a discrete probability distribution which is contrast to the binomial distribution.
- A Hypergeometric random variable is the number of successes that result from a Hypergeometric experiment.
- The probability distribution of a Hypergeometric random variable is called a Hypergeometric Distribution.
- In HYPGEOMDIST(n1,n2,n3,n4) where n1 is the number of items in the Sample that are classified as successes.
- is the total number of items in the sample.
- is the number of items in the population that are classified as successes and is the total number of items in the sample.
- The following conditions are applied to the Hypergeometric distribution:
1.This distribution is applies to sampling without replacement from a finite population whose elements can be classified into two categories like Success or Failure. 2.The population or set to be sampled consists of N individuals, objects,or elements 3.Each individual can be success (S) or a failure (F),
and there are M successes in the population.
4.A sample of n individuals is selected without replacement in such a way that each subset of size n is equally likely to be chosen.
- The Hyper geometric probability distribution is:
for is an integer satisfying . where is sample's success.
- is the sample's size.
- is population's success and is the population size.
- Here we can give any positive real numbers.
- Suppose we are assigning any decimals numbers it will change in to Integers.
- This function will give result as error when
1.Any one of the argument is non-numeric. 2. or n1 is greater than the smaller value of n2 or n3. 3. is less than the bigger of 0 or(n2-n4+n3) 4. or 5. or or
Examples
Draw 6 cards from a deck without replacement. What is the probability of getting two hearts? Here M = 13 number of hearts N = 52 total number of cards so N-M= 52-13= 39 and x=2,n=6 so n-x=6-2=4 HYPGEOMDIST(2,6,13,52)=0.315129882 2.42 balls are numbered 1 - 42. You select six numbers between 1 and 42. What is the probability that they contain (i)match 3? (ii) match 4? (i)Here M= 6,N=42,x=3and n=6 HYPGEOMDIST(3,6,6,42)=0.02722185 (ii)Here M= 6,N=42,x=4and n=6 HYPGEOMDIST(4,6,6,42)=0.001801446 3.
 is the sample's success.
is the sample's success.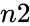 is the sample's size.
is the sample's size.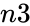 is population's success.
is population's success.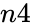 is the population size.
is the population size.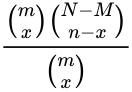
 is an integer satisfying
is an integer satisfying 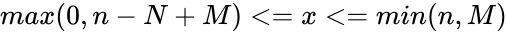 . where
. where  is the sample's size.
is the sample's size. is population's success and
is population's success and 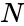 is the population size.
is the population size.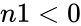 or n1 is greater than the smaller value of n2 or n3.
3.
or n1 is greater than the smaller value of n2 or n3.
3.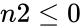 or
or 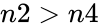 5.
5.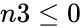 or
or 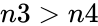 or
or