Difference between revisions of "Manuals/calci/IMLN"
Jump to navigation
Jump to search
| Line 4: | Line 4: | ||
==Description== | ==Description== | ||
*This function gives the Natural Logarithm of a complex number. | *This function gives the Natural Logarithm of a complex number. | ||
| − | *In IMLN(z), where <math>z<math> is the complex number in the form of <math>x+iy</math>. i.e <math>x<math> & <math>y<math> are the real numbers. | + | *In IMLN(z), where <math>z</math> is the complex number in the form of <math>x+iy</math>. i.e <math>x<math> & <math>y</math> are the real numbers. |
| − | *<math>I</math> imaginary unit <math>i=sqrt{-1}<math>. | + | *<math>I</math> imaginary unit <math>i=sqrt{-1}</math>. |
*A logarithm of <math>z</math> is a complex number w such that <math>z = e^w</math> and it is denoted by <math>ln(z)</math>. | *A logarithm of <math>z</math> is a complex number w such that <math>z = e^w</math> and it is denoted by <math>ln(z)</math>. | ||
| − | *If <math>z = x+iy</math> with <math>x<math> & <math>y</math> are real numbers then natural logarithm of a complex number : | + | *If <math>z = x+iy</math> with <math>x</math> & <math>y</math> are real numbers then natural logarithm of a complex number : |
<math>ln(z)= w = ln(|z|) + iarg(z) = ln(\sqrt{x^2+y^2}+itan^{-1}(\frac{y}{x}</math> adding integer multiples of <math>2\pi i</math> gives all the others. | <math>ln(z)= w = ln(|z|) + iarg(z) = ln(\sqrt{x^2+y^2}+itan^{-1}(\frac{y}{x}</math> adding integer multiples of <math>2\pi i</math> gives all the others. | ||
*We can use COMPLEX function to convert real and imaginary number in to a complex number. | *We can use COMPLEX function to convert real and imaginary number in to a complex number. | ||
Revision as of 05:12, 16 December 2013
IMLN(z)
- is the complex number is of the form
Description
- This function gives the Natural Logarithm of a complex number.
- In IMLN(z), where is the complex number in the form of . i.e Failed to parse (syntax error): {\displaystyle x<math> & <math>y} are the real numbers.
- imaginary unit .
- A logarithm of is a complex number w such that and it is denoted by .
- If with & are real numbers then natural logarithm of a complex number :
adding integer multiples of gives all the others.
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
Examples
- IMLN("3-2i")=1.28247467873077-0.588002603547568i
- IMLN("6+7i")=2.22132562824516+0.862170054667226i
- IMLN("4")=1.38629436111989 But calci is not considering the zero value of imaginary value of z.
- IMLN("10i")=2.30258509299405+1.5707963267949i
See Also
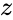 is the complex number is of the form
is the complex number is of the form 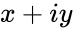
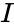 imaginary unit
imaginary unit 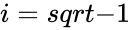 .
.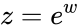 and it is denoted by
and it is denoted by 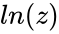 .
.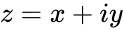 with
with  &
& 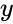 are real numbers then natural logarithm of a complex number :
are real numbers then natural logarithm of a complex number :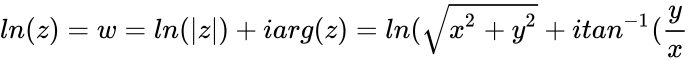 adding integer multiples of
adding integer multiples of 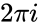 gives all the others.
gives all the others.