Difference between revisions of "Manuals/calci/NORMINV"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''NORMINV'''('''p''','''m''','''sd''') '''Where p''' is a probability corresponding to the normal distribution ...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''NORMINV(prob,m,sd)'''</div><br/> |
| + | *<math>prob</math> is the probability corresponding to the normal distribution,<math>m</math> is the mean , and <math>sd</math> is the standard deviation. | ||
| − | + | ==Description== | |
| + | *This function gives the inverse of the normal cumulative distribution for the particular mean and standard deviation. | ||
| + | *If <math>NORMDIST(x,m,sd,TRUE)=prob</math>, then <math>NORMINV(prob,m,sd)=x</math>. | ||
| + | *<math>NORMINV</math> using the iterating method to find the value of x. | ||
| + | *Suppose the iteration has not converged after 100 searches, then the function gives the error result. | ||
| + | *In <math>NORMINV(prob,m,sd)</math>, where <math>prob</math> is the corresponding probability of the normal distribution, <math>m</math> is the arithmetic mean of the normal distribution and <math>sd</math> is the standard deviation of the normal distribution. | ||
| + | *This function will return the result as error when | ||
| + | 1. any one of the argument is nonnumeric | ||
| + | 2.Suppose prob<0 or prob>1 | ||
| + | 3.sd<=0. | ||
| + | *If m=0 and sd=1,NORMINV uses the standard normal distribution. | ||
| − | + | ==Examples== | |
| + | #NORMINV(0.01884908749,17.4,3.2)=10.750011 | ||
| + | #NORMINV(0.998742,5.4,2.3)=12.349244172 | ||
| + | #NORMINV(1,7.2,2.3)=NULL | ||
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/NORMDIST | NORMDIST ]] | |
| − | + | *[[Manuals/calci/NORMSDIST | NORMSDIST ]] | |
| + | *[[Manuals/calci/NORMSINV | NORMSINV ]] | ||
| − | + | ==References== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 03:49, 1 January 2014
NORMINV(prob,m,sd)
- is the probability corresponding to the normal distribution, is the mean , and is the standard deviation.
Description
- This function gives the inverse of the normal cumulative distribution for the particular mean and standard deviation.
- If , then .
- using the iterating method to find the value of x.
- Suppose the iteration has not converged after 100 searches, then the function gives the error result.
- In , where is the corresponding probability of the normal distribution, is the arithmetic mean of the normal distribution and is the standard deviation of the normal distribution.
- This function will return the result as error when
1. any one of the argument is nonnumeric 2.Suppose prob<0 or prob>1 3.sd<=0.
- If m=0 and sd=1,NORMINV uses the standard normal distribution.
Examples
- NORMINV(0.01884908749,17.4,3.2)=10.750011
- NORMINV(0.998742,5.4,2.3)=12.349244172
- NORMINV(1,7.2,2.3)=NULL
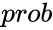 is the probability corresponding to the normal distribution,
is the probability corresponding to the normal distribution, is the mean , and
is the mean , and 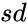 is the standard deviation.
is the standard deviation.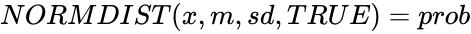 , then
, then 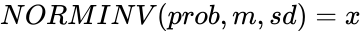 .
. using the iterating method to find the value of x.
using the iterating method to find the value of x.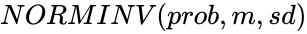 , where
, where