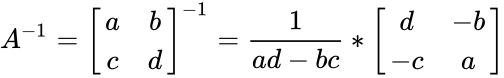Difference between revisions of "Manuals/calci/MINVERSE"
Jump to navigation
Jump to search
| Line 9: | Line 9: | ||
*Let <math>A<math> be the 2x2 matrix with the elements A=|a b | *Let <math>A<math> be the 2x2 matrix with the elements A=|a b | ||
c d|. | c d|. | ||
| − | *Then the inverse of matrix <math>A<math> is denoted by A^-1.So A^-1= | + | *Then the inverse of matrix <math>A</math> is denoted by <math>A^{-1}</math>.So <math>A^{-1}=\begin{bmatrix} |
| − | + | a & b \\ | |
| + | c & d \\ | ||
| + | \end{bmatrix}^{-1}= \frac{1}{ad-bc} * \begin{bmatrix} | ||
| + | d & -b \\ | ||
| + | -c & a \\ | ||
| + | \end{bmatrix} </math> | ||
| + | </math> | ||
*Now let A be the matrix is of order nXn. | *Now let A be the matrix is of order nXn. | ||
*Then the inverse of A is A^-1= 1/det(A) . adj(A) | *Then the inverse of A is A^-1= 1/det(A) . adj(A) | ||
Revision as of 04:56, 1 January 2014
MINVERSE(arr)
- is the array of numeric elements
Description
- This function gives the inverse matrix for the given matrix.
- We have to find a inverse of a matrix then it should satisfy the following conditions
- 1.A matrix must be a square matrix.
- 2.It's determinant not equal to 0.
- Let is denoted by .So
</math>
- Now let A be the matrix is of order nXn.
- Then the inverse of A is A^-1= 1/det(A) . adj(A)
- Where adj(A) is the adjoint of A.
- Adjoint is the matrix formed by taking the transpose of the co-factor matrix of a given original matrix.
- Also A.A^-1=A^-1.A=I, where I is the identity matrix.Non-square matrices do not have inverses.
- Not all square matrices have inverses.
- A square matrix which has an inverse is called invertible or non-singular, and a square matrix without an inverse is called non-invertible or singular.
- This function will return the result as error when
1. Any one of the cell is non-numeric or any cell is empty or contain text 2. Suppose number of rows not equal to number of columns
Examples
Matrix A A=(4 3
3 2)
MINVERSE(B5:C6)=(-2 3
3 -4)
MATRIX A A=(3 4
6 8)
MINVERSE(C4:D5)=Null, because its det value is 0. MATRIX A A=(2 3
4 7)
MINVERSE(B4:C5)=(3.5 -1.5
-2 1)
 is the array of numeric elements
is the array of numeric elements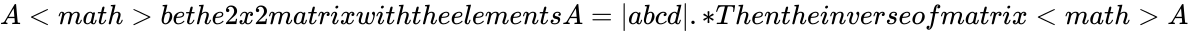 is denoted by
is denoted by 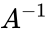 .So
.So