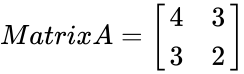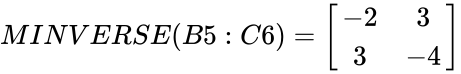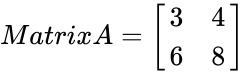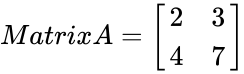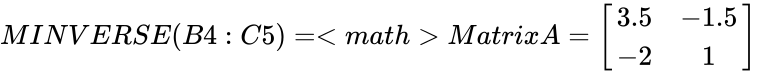Difference between revisions of "Manuals/calci/MINVERSE"
Jump to navigation
Jump to search
| Line 40: | Line 40: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| + | <math> | ||
MINVERSE(B5:C6)= | MINVERSE(B5:C6)= | ||
| − | |||
\begin{bmatrix} | \begin{bmatrix} | ||
-2 & 3 \\ | -2 & 3 \\ | ||
| Line 47: | Line 47: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| − | + | ||
| − | A= | + | <math>Matrix A= |
| − | + | \begin{bmatrix} | |
| − | MINVERSE(C4:D5)=Null, because its | + | 3 & 4 \\ |
| − | + | 6 & 8 \\ | |
| − | A= | + | \end{bmatrix} |
| − | + | </math> | |
| − | MINVERSE(B4:C5)= | + | |
| − | + | MINVERSE(C4:D5)=Null, because its determinant value is 0. | |
| + | |||
| + | <math>Matrix A= | ||
| + | \begin{bmatrix} | ||
| + | 2 & 3 \\ | ||
| + | 4 & 7 \\ | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | <math>MINVERSE(B4:C5)=<math>Matrix A= | ||
| + | \begin{bmatrix} | ||
| + | 3.5 & -1.5 \\ | ||
| + | -2 & 1 \\ | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
==See Also== | ==See Also== | ||
Revision as of 05:17, 1 January 2014
MINVERSE(arr)
- is the array of numeric elements
Description
- This function gives the inverse matrix for the given matrix.
- We have to find a inverse of a matrix then it should satisfy the following conditions
- 1.A matrix must be a square matrix.
- 2.It's determinant not equal to 0.
- Let be the 2x2 matrix with the elements
.
- Then the inverse of matrix is denoted by .
- Now let be the matrix is of order .
- Then the inverse of is
- Where is the adjoint of .
- Adjoint is the matrix formed by taking the Transpose of the Co-factor matrix of the original matrix.
- Also , where is the identity matrix.
- Non-square matrices do not have inverses.
- Not all square matrices have inverses.
- A square matrix which has an inverse is called invertible or non-singular, and a square matrix without an inverse is called non-invertible or singular.
- This function will return the result as error when
1. Any one of the cell is non-numeric or any cell is empty or contain text 2. Suppose number of rows not equal to number of columns
Examples
MINVERSE(C4:D5)=Null, because its determinant value is 0.
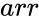 is the array of numeric elements
is the array of numeric elements be the 2x2 matrix with the elements
be the 2x2 matrix with the elements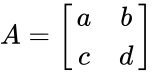 .
.
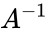 .
.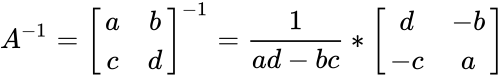
 .
.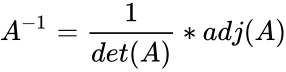
 is the adjoint of
is the adjoint of 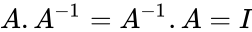 , where
, where 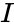 is the identity matrix.
is the identity matrix.