Difference between revisions of "Manuals/calci/TTESTEQUALVARIANCES"
Jump to navigation
Jump to search
| Line 11: | Line 11: | ||
*1.The two sample sizes are equal; | *1.The two sample sizes are equal; | ||
*2.It can be assumed that the two distributions have the same variance. | *2.It can be assumed that the two distributions have the same variance. | ||
| − | *In <math>TTESTTWOSAMPLESEQUALVARIANCES(ar1,ar2,md,alpha,lv), ar1 </math> and <math> ar2 </math> are two arrays of sample values. <math> md </math> is the Hypothesized Mean Difference . | + | *In <math>TTESTTWOSAMPLESEQUALVARIANCES(ar1,ar2,md,alpha,lv)</math>, <math>ar1 </math> and <math> ar2 </math> are two arrays of sample values. <math> md </math> is the Hypothesized Mean Difference . |
*Suppose md=0 which indicates that sample means are hypothesized to be equal. | *Suppose md=0 which indicates that sample means are hypothesized to be equal. | ||
*<math> alpha </math> is the significance level which ranges from 0 to 1. | *<math> alpha </math> is the significance level which ranges from 0 to 1. | ||
| Line 18: | Line 18: | ||
*The t statistic of this function calculated by: | *The t statistic of this function calculated by: | ||
<math>t = \frac{\bar{x_1}-\bar{x_2}}{s_{x1}.s_{x2}.\sqrt{\frac{2}{n}}}</math> | <math>t = \frac{\bar{x_1}-\bar{x_2}}{s_{x1}.s_{x2}.\sqrt{\frac{2}{n}}}</math> | ||
| − | + | where <math>s_{x1}.s_{x2} = \sqrt{\frac{1}{2}(s_{x1}^2+s_{x2}^2)}</math> | |
| − | *Here <math>s_x_1</math> and <math>s_x_2</math> are unbiased estimators of the variances of two samples.<math> | + | *Here <math>s_x_1</math> and <math>s_x_2</math> are unbiased estimators of the variances of two samples.<math>s_{x1}.s_{x2}</math> is the grand standard deviation data 1 and data2 and n is the data points of two data set. |
*This function will give the result as error when | *This function will give the result as error when | ||
| − | 1.any one of the argument is | + | 1.any one of the argument is non-numeric. |
2.alpha>1 | 2.alpha>1 | ||
| − | 3.ar1 and ar2 are having different number of data points. | + | 3.<math>ar1 </math> and <math> ar2 </math> are having different number of data points. |
==Examples== | ==Examples== | ||
Revision as of 23:15, 3 February 2014
TTESTTWOSAMPLESEQUALVARIANCES(ar1,ar2,md,alpha,lv)
- and are set of values.
- is the Hypothesized Mean Difference.
- is the significance level.
- is the logical value.
Description
- This function calculating the two Sample for equal variances determines whether two sample means are equal.
- We can use this test when both:
- 1.The two sample sizes are equal;
- 2.It can be assumed that the two distributions have the same variance.
- In , and are two arrays of sample values. is the Hypothesized Mean Difference .
- Suppose md=0 which indicates that sample means are hypothesized to be equal.
- is the significance level which ranges from 0 to 1.
- is the logical value like TRUE or FALSE.
- TRUE is indicating the result will display in new worksheet.Suppose we are omitted the lv value it will consider the value as FALSE.
- The t statistic of this function calculated by:
where
- Here Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. TeX parse error: Double subscripts: use braces to clarify"): {\displaystyle s_{x}_{1}} and Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. TeX parse error: Double subscripts: use braces to clarify"): {\displaystyle s_{x}_{2}} are unbiased estimators of the variances of two samples. is the grand standard deviation data 1 and data2 and n is the data points of two data set.
- This function will give the result as error when
1.any one of the argument is non-numeric. 2.alpha>1 3. and are having different number of data points.
Examples
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 10 | 15 | 18 | 27 | 12 | 34 |
| 2 | 17 | 20 | 25 | 39 | 9 | 14 |
- =TTESTSAMPLESEQUALVARIANCES(A1:F1,A2:F2,2,0.5)
See Also
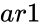 and
and 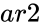 are set of values.
are set of values.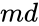 is the Hypothesized Mean Difference.
is the Hypothesized Mean Difference.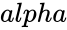 is the significance level.
is the significance level. is the logical value.
is the logical value.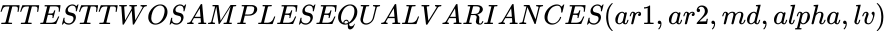 ,
, 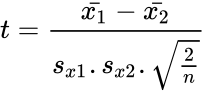
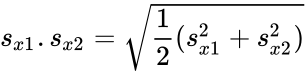
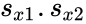 is the grand standard deviation data 1 and data2 and n is the data points of two data set.
is the grand standard deviation data 1 and data2 and n is the data points of two data set.