Difference between revisions of "Manuals/calci/IRR"
Jump to navigation
Jump to search
| Line 24: | Line 24: | ||
|+1..10@SQRT | |+1..10@SQRT | ||
|- | |- | ||
| − | ! !! A !! B | + | ! !! A !! B |
| − | |||
|- | |- | ||
| − | | -100000 || -500000 | + | ! 1 |
| − | + | | -100000 || -500000 | |
|- | |- | ||
| + | ! 2 | ||
| 10000 || 32000 | | 10000 || 32000 | ||
| + | |- | ||
! 3 | ! 3 | ||
| + | |28000 || 45000 | ||
|- | |- | ||
| − | |||
! 4 | ! 4 | ||
| + | |20000 || 100000 | ||
|- | |- | ||
| − | |||
! 5 | ! 5 | ||
| + | | 32500 || 150000 | ||
|- | |- | ||
| − | |||
! 6 | ! 6 | ||
| + | | 59000 || 275000 | ||
|- | |- | ||
| − | + | ! 7 | |
| − | ! 7 | ||
| − | |||
|1000 ||67000 | |1000 ||67000 | ||
|} | |} | ||
| Line 52: | Line 52: | ||
#=IRR(B1:B7) = 6.7% | #=IRR(B1:B7) = 6.7% | ||
#=IRR(B1:B5,5%)= -160.99% | #=IRR(B1:B5,5%)= -160.99% | ||
| − | |||
==See Also== | ==See Also== | ||
Revision as of 00:39, 31 March 2014
IRR(v,g)
- is the array of values.
- is the number is close to the result of IRR.
Description
- This function gives the internal rate of return of a cash flow stream associated with an investment.
- The Internal Rate of Return is the interest rate that makes the Net Present Value zero.
- is similar to the net present value calculation.
- In , is an values which is the array or a reference to cells that contain numbers for which you want to calculate the internal rate of return.
- is the guess which is indicating the number that you guess is close to the result of .
- must have atleast one positive and one negative value to find the internal rate of return.
- The value of can be array or reference argument contains text, logical values or empty cells, the values which are ignored.
- The value is optional, when we are omitting the value,by default it will consider the value as 10%(0.1).
- The calculation of uses an iterative method.
- The value is starting from g value and doing the calculation until the result is accurate within 0.00001%.
- Also can't find the result that works after 20 tries.
- The calculating for cash flows occurring at any other regular intervals like quarterly or semi annual by using respective factor.
- is also called effective interest rate, or rate of return.
- It is used to evaluate an investment or project.
- The function will return the result as error after the 20 tries in the iterative method.
Examples
| A | B | |
|---|---|---|
| 1 | -100000 | -500000 |
| 2 | 10000 | 32000 |
| 3 | 28000 | 45000 |
| 4 | 20000 | 100000 |
| 5 | 32500 | 150000 |
| 6 | 59000 | 275000 |
| 7 | 1000 | 67000 |
- =IRR(A1:A6)=11.88%
- =IRR(A1:A5,20%) = -3.45%
- =IRR(B1:B7) = 6.7%
- =IRR(B1:B5,5%)= -160.99%
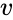 is the array of values.
is the array of values.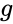 is the number is close to the result of IRR.
is the number is close to the result of IRR. is similar to the net present value calculation.
is similar to the net present value calculation.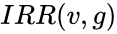 ,
,