Difference between revisions of "Manuals/calci/SIGNTEST"
Jump to navigation
Jump to search
(Created page with "==Feature==") |
|||
| Line 1: | Line 1: | ||
| − | == | + | <div style="font-size:25px">'''SIGNTEST(Array,Median,AlternateHypothesis,LogicalValue)'''</div><br/> |
| + | *<math>Array</math> is the set of values to find the statistic value. | ||
| + | *<math>Median</math> is the median of the array of values. | ||
| + | *<math>AlternateHypothesis</math> is the alternate hypothesis of the array. | ||
| + | *<math>Logicalvalue</math> is either TRUE or FALSE. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the test statistic of the Sign test. | ||
| + | *The Sign Test is ued to test the Hypothesis that there is no difference between two continuous distributions X and Y. | ||
| + | *This test is one type of the Non parametric Test. | ||
| + | *The sign test is designed to test a hypothesis about the location of a population distribution. | ||
| + | *The Sign test does not require the assumption that the population is normally distributed. | ||
| + | *The normality of the distribution is doubtable, then Sign test is used to find the statitic instead of one sample T-test. | ||
| + | *The sign test uses the sign of the differences, unlike the paired t test which uses the sign and magnitude of the differences. | ||
| + | *To perform this test, Consider the independent pairs of sample data from the populations{(x1,y1)(x2,y2).....(xn,yn)}. | ||
| + | *From this pair,it must be omitted with no differences(xi=yi) | ||
| + | *The Sign test data are having the following properties: | ||
| + | *1.The differences of pairs are assumed to be independent. | ||
| + | *2.Each pairs comes from the same continuous population. | ||
| + | *3.The values <math>X_i</math> and <math>Y_i</math> represent are ordered , so the comparisons "greater than", "less than", and "equal to" are meaningful. | ||
| + | *The test statistic is expected to follow a binomial distribution, the standard binomial test is used to calculate significance. | ||
| + | *The sign test can also be viewed as testing the hypothesis that the median of the differences is zero. | ||
| + | *The sign test Hypothesis is having the following steps: | ||
| + | *'''Step1''':State Null and Alternative Hypothesis | ||
| + | *Two ways to state these: One sample or sample of differences, want to test specific value for the population median M. | ||
| + | *Null: H0:p=1/2is equivalent to M = M0. | ||
| + | *Alternative: <math>Ha:p<1/2</math> is equivalent to <math>M>M_0</math> or <math>Ha: p>1/2</math> is equivalent to <math>M < M_0</math> or Ha:p not equal to 1/2 is equivalent to <math>M\ne M_0</math> | ||
| + | *'''Step2''':Test statistic (no data conditions needed) | ||
| + | *S+ = Number of observations greater than <math>M_0</math> or Number of observations with <math>x>y</math>. | ||
| + | *S− = Number of observations less than <math>M_0</math> or Number of observations with <math>x<y</math>. | ||
| + | *Ties are not used, so use n = S+ + S−. | ||
| + | *'''Step3''': Finding the p-value | ||
| + | *Remember, p-value is: | ||
| + | ** Probability of observing a test statistic as large as or larger than that observed | ||
| + | ** in the direction that supports Ha | ||
| + | ** if the null hypothesis is true. | ||
| + | *'''Step 4''':Use tables of the binomial distribution to find the probability of observing a value of | ||
| + | r or higher assuming p = 1/2 and <math>n = n_0</math>. | ||
| + | *If the test is one-sided, this is your p-value. | ||
| + | *'''Step5''': If the test is a two-sided test, double the probability to obtain the p-value. | ||
Revision as of 02:43, 16 May 2014
SIGNTEST(Array,Median,AlternateHypothesis,LogicalValue)
- is the set of values to find the statistic value.
- is the median of the array of values.
- is the alternate hypothesis of the array.
- is either TRUE or FALSE.
Description
- This function gives the test statistic of the Sign test.
- The Sign Test is ued to test the Hypothesis that there is no difference between two continuous distributions X and Y.
- This test is one type of the Non parametric Test.
- The sign test is designed to test a hypothesis about the location of a population distribution.
- The Sign test does not require the assumption that the population is normally distributed.
- The normality of the distribution is doubtable, then Sign test is used to find the statitic instead of one sample T-test.
- The sign test uses the sign of the differences, unlike the paired t test which uses the sign and magnitude of the differences.
- To perform this test, Consider the independent pairs of sample data from the populations{(x1,y1)(x2,y2).....(xn,yn)}.
- From this pair,it must be omitted with no differences(xi=yi)
- The Sign test data are having the following properties:
- 1.The differences of pairs are assumed to be independent.
- 2.Each pairs comes from the same continuous population.
- 3.The values and represent are ordered , so the comparisons "greater than", "less than", and "equal to" are meaningful.
- The test statistic is expected to follow a binomial distribution, the standard binomial test is used to calculate significance.
- The sign test can also be viewed as testing the hypothesis that the median of the differences is zero.
- The sign test Hypothesis is having the following steps:
- Step1:State Null and Alternative Hypothesis
- Two ways to state these: One sample or sample of differences, want to test specific value for the population median M.
- Null: H0:p=1/2is equivalent to M = M0.
- Alternative: is equivalent to or is equivalent to or Ha:p not equal to 1/2 is equivalent to
- Step2:Test statistic (no data conditions needed)
- S+ = Number of observations greater than or Number of observations with .
- S− = Number of observations less than or Number of observations with .
- Ties are not used, so use n = S+ + S−.
- Step3: Finding the p-value
- Remember, p-value is:
- Probability of observing a test statistic as large as or larger than that observed
- in the direction that supports Ha
- if the null hypothesis is true.
- Step 4:Use tables of the binomial distribution to find the probability of observing a value of
r or higher assuming p = 1/2 and .
- If the test is one-sided, this is your p-value.
- Step5: If the test is a two-sided test, double the probability to obtain the p-value.
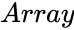 is the set of values to find the statistic value.
is the set of values to find the statistic value.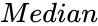 is the median of the array of values.
is the median of the array of values.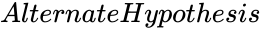 is the alternate hypothesis of the array.
is the alternate hypothesis of the array.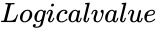 is either TRUE or FALSE.
is either TRUE or FALSE.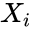 and
and  represent are ordered , so the comparisons "greater than", "less than", and "equal to" are meaningful.
represent are ordered , so the comparisons "greater than", "less than", and "equal to" are meaningful.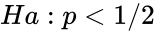 is equivalent to
is equivalent to 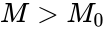 or
or 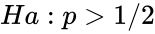 is equivalent to
is equivalent to 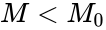 or Ha:p not equal to 1/2 is equivalent to
or Ha:p not equal to 1/2 is equivalent to 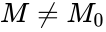
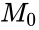 or Number of observations with
or Number of observations with 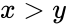 .
. .
.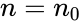 .
.