Difference between revisions of "Manuals/calci/HESSENBERG"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''HESSENBERG'''</div><br/>") |
|||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''HESSENBERG'''</div><br/> | + | <div style="font-size:30px">'''MATRIX("HESSENBERG",order)'''</div><br/> |
| + | *<math>order</math> is the order of the Hessenberg matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the matrix with the property of Hessenberg matrix. | ||
| + | *A Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular. | ||
| + | *To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal. | ||
| + | *Here MATRIX("hessenberg") displays the hessenberg matrix of order 3. | ||
| + | *An nxn matrix with a_i,j=0 for i>j+1 is called a Hessenberg matrix. | ||
| + | *So the form of a Hessenberg matrix is: | ||
| + | *So the matrix is zero below the first subdiagonal. | ||
| + | *If the matrix is symmetric or Hermitian, the form is tridiagonal. | ||
| + | |||
| + | \begin{bmatrix} | ||
| + | a_{11} & a_{12} & a_{13} \cdots & a_{1(n-1)}& a_{1n} \\ | ||
| + | a_{21} & a_{22} & a_{23} \cdots& a_{2(n-1)}& a_{2n} \\ | ||
| + | 0 & a_{32} & a_{33} \cdots& a_{3(n-1)}& a_{3n} \\ | ||
| + | 0 & 0 & a_{43} \cdots& a_{4(n-1)}& a_{4n} \\ | ||
| + | 0 & 0 & 0 \cdots& a_{5(n-1)}& a_{5n} \\ | ||
| + | \vdots & \ddots & \vdots \\ | ||
| + | 0 & 0 & 0 & a_{(n-1)(n-2)} & a_{(n-1)(n-1)} & a_{(n-1)n}\\ | ||
| + | 0 & 0 & 0 & 0 & a_{n(n-1)} & a_{nn}\\ | ||
| + | \end{bmatrix} | ||
Revision as of 11:44, 24 April 2015
MATRIX("HESSENBERG",order)
- is the order of the Hessenberg matrix.
Description
- This function gives the matrix with the property of Hessenberg matrix.
- A Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular.
- To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal.
- Here MATRIX("hessenberg") displays the hessenberg matrix of order 3.
- An nxn matrix with a_i,j=0 for i>j+1 is called a Hessenberg matrix.
- So the form of a Hessenberg matrix is:
- So the matrix is zero below the first subdiagonal.
- If the matrix is symmetric or Hermitian, the form is tridiagonal.
\begin{bmatrix} a_{11} & a_{12} & a_{13} \cdots & a_{1(n-1)}& a_{1n} \\ a_{21} & a_{22} & a_{23} \cdots& a_{2(n-1)}& a_{2n} \\ 0 & a_{32} & a_{33} \cdots& a_{3(n-1)}& a_{3n} \\ 0 & 0 & a_{43} \cdots& a_{4(n-1)}& a_{4n} \\ 0 & 0 & 0 \cdots& a_{5(n-1)}& a_{5n} \\ \vdots & \ddots & \vdots \\ 0 & 0 & 0 & a_{(n-1)(n-2)} & a_{(n-1)(n-1)} & a_{(n-1)n}\\ 0 & 0 & 0 & 0 & a_{n(n-1)} & a_{nn}\\ \end{bmatrix}
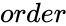 is the order of the Hessenberg matrix.
is the order of the Hessenberg matrix.