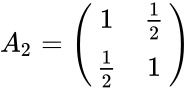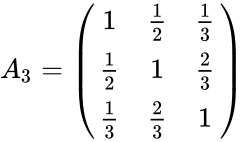Difference between revisions of "Manuals/calci/LEHMER"
Jump to navigation
Jump to search
| Line 4: | Line 4: | ||
==Description== | ==Description== | ||
*This function gives the lehmer matrix of order 3. | *This function gives the lehmer matrix of order 3. | ||
| − | *The the n×n Lehmer matrix, is the constant symmetric matrix defined by <math>a_{ij}=\frac{min {i,j} }{max {i,j} } = | + | *The the n×n Lehmer matrix, is the constant symmetric matrix defined by <math>a_{ij}=\frac\left \{min {i,j}\right\}\left\{{max {i,j}\right\ } = |
\begin{cases} \frac{i}{j} & j\ge i \\ | \begin{cases} \frac{i}{j} & j\ge i \\ | ||
| − | \frac{j}{i} & j > i | + | \frac{j}{i} & j > i |
\end{cases} </math> | \end{cases} </math> | ||
*Also the inverse of a Lehmer matrix is a tridiagonal matrix and is known to be symmetric tridiagonal. | *Also the inverse of a Lehmer matrix is a tridiagonal matrix and is known to be symmetric tridiagonal. | ||
Revision as of 08:57, 30 April 2015
MATRIX("LEHMER",order)
- is the order of the Lehmer matrix.
Description
- This function gives the lehmer matrix of order 3.
- The the n×n Lehmer matrix, is the constant symmetric matrix defined by Failed to parse (syntax error): {\displaystyle a_{ij}=\frac\left \{min {i,j}\right\}\left\{{max {i,j}\right\ } = \begin{cases} \frac{i}{j} & j\ge i \\ \frac{j}{i} & j > i \end{cases} }
- Also the inverse of a Lehmer matrix is a tridiagonal matrix and is known to be symmetric tridiagonal.
- And the value of this matrix have strictly negative entries (i.e., with positive eigenvalues).
- Example of 2x2 and 3x3 lehmer matrices and its inverses are
 is the order of the Lehmer matrix.
is the order of the Lehmer matrix.