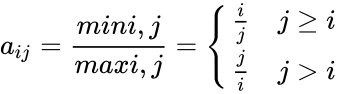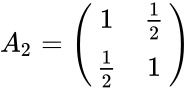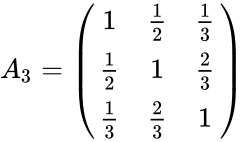Difference between revisions of "Manuals/calci/LEHMER"
Jump to navigation
Jump to search
| Line 20: | Line 20: | ||
\frac{1}{3} & \frac{2}{3} & 1 \\ | \frac{1}{3} & \frac{2}{3} & 1 \\ | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
| + | |||
| + | |||
| + | ==Examples== | ||
| + | *MATRIX("lehmer") | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 0.5 || 0.3333333333333333 | ||
| + | |- | ||
| + | | 0.5 || 1 || 0.6666666666666666 | ||
| + | |- | ||
| + | | 0.3333333333333333 || 0.6666666666666666 || 1 | ||
| + | |} | ||
| + | *MATRIX("lehmer",6) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 0.5 || 0.3333333333333333 || 0.25 || 0.2 || 0.16666666666666666 | ||
| + | |- | ||
| + | | 0.5 || 1 || 0.6666666666666666 || 0.5 || 0.4 || 0.3333333333333333 | ||
| + | |- | ||
| + | | 0.3333333333333333 || 0.6666666666666666 || 1 || 0.75 || 0.6 || 0.5 | ||
| + | |- | ||
| + | | 0.25 || 0.5 || 0.75 || 1 || 0.8 || 0.6666666666666666 | ||
| + | |- | ||
| + | | 0.2 || 0.4 || 0.6 || 0.8 || 1 || 0.8333333333333334 | ||
| + | |- | ||
| + | | 0.16666666666666666 ||0.3333333333333333 || 0.5 || 0.6666666666666666 || 0.8333333333333334 || 1 | ||
| + | |} | ||
Revision as of 09:27, 30 April 2015
MATRIX("LEHMER",order)
- is the order of the Lehmer matrix.
Description
- This function gives the lehmer matrix of order 3.
- The the n×n Lehmer matrix, is the constant symmetric matrix defined by
- Also the inverse of a Lehmer matrix is a tridiagonal matrix and is known to be symmetric tridiagonal.
- And the value of this matrix have strictly negative entries (i.e., with positive eigenvalues).
- Example of 2x2 and 3x3 lehmer matrices are
Examples
- MATRIX("lehmer")
| 1 | 0.5 | 0.3333333333333333 |
| 0.5 | 1 | 0.6666666666666666 |
| 0.3333333333333333 | 0.6666666666666666 | 1 |
- MATRIX("lehmer",6)
| 1 | 0.5 | 0.3333333333333333 | 0.25 | 0.2 | 0.16666666666666666 |
| 0.5 | 1 | 0.6666666666666666 | 0.5 | 0.4 | 0.3333333333333333 |
| 0.3333333333333333 | 0.6666666666666666 | 1 | 0.75 | 0.6 | 0.5 |
| 0.25 | 0.5 | 0.75 | 1 | 0.8 | 0.6666666666666666 |
| 0.2 | 0.4 | 0.6 | 0.8 | 1 | 0.8333333333333334 |
| 0.16666666666666666 | 0.3333333333333333 | 0.5 | 0.6666666666666666 | 0.8333333333333334 | 1 |
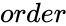 is the order of the Lehmer matrix.
is the order of the Lehmer matrix.