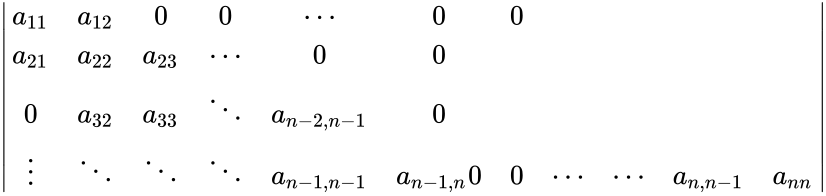Difference between revisions of "Manuals/calci/TRIDIAGONAL"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''TRIDIAGONAL'''</div><br/>") |
|||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''TRIDIAGONAL'''</div><br/> | + | <div style="font-size:30px">'''MATRIX("TRIDIAGONAL",order)'''</div><br/> |
| + | *<math>order</math> is the size of the Tridiagonal matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function returns the matrix with the property of tridiagonal. | ||
| + | *A square matrix with nonzero elements only on the diagonal and slots horizontally or vertically adjacent the diagonal. | ||
| + | *i.e., along the subdiagonal and superdiagonal. | ||
| + | *So a tridiagonal matrix is a matrix that has nonzero elements only on the main diagonal, the first diagonal below this, and the first diagonal above the main diagonal. | ||
| + | *A tridiagonal is of the form: | ||
| + | <math>\begin{vmatrix} | ||
| + | a_{11} & a_{12} & 0 & 0 & \cdots & 0 & 0 \\ | ||
| + | a_{21} & a_{22} & a_{23} & \cdots & 0 & 0 \\ | ||
| + | 0 & a_{32} & a_{33} & \ddots & a_{n-2,n-1} & 0 \\ | ||
| + | \vdots &\ddots & \ddots & \ddots & a_{n-1,n-1} & a_{n-1,n} | ||
| + | 0 & 0 & \cdots &\cdots & a_{n,n-1} & a_{nn} | ||
| + | \end{vmatrix}</math> | ||
| + | *A general tridiagonal matrix is not necessarily symmetric or Hermitian,but tridiagonal matrix is a matrix that is both upper and lower Hessenberg matrix. | ||
| + | *In Calci, MATRIX("tridiagonal") gives the tridiagonal matirx of order 3. | ||
| + | *Users can change the order of the matrix. | ||
Revision as of 10:32, 7 May 2015
MATRIX("TRIDIAGONAL",order)
- is the size of the Tridiagonal matrix.
Description
- This function returns the matrix with the property of tridiagonal.
- A square matrix with nonzero elements only on the diagonal and slots horizontally or vertically adjacent the diagonal.
- i.e., along the subdiagonal and superdiagonal.
- So a tridiagonal matrix is a matrix that has nonzero elements only on the main diagonal, the first diagonal below this, and the first diagonal above the main diagonal.
- A tridiagonal is of the form:
- A general tridiagonal matrix is not necessarily symmetric or Hermitian,but tridiagonal matrix is a matrix that is both upper and lower Hessenberg matrix.
- In Calci, MATRIX("tridiagonal") gives the tridiagonal matirx of order 3.
- Users can change the order of the matrix.
 is the size of the Tridiagonal matrix.
is the size of the Tridiagonal matrix.