Difference between revisions of "Manuals/calci/ZTEST"
Jump to navigation
Jump to search
| Line 3: | Line 3: | ||
*<math>x</math> is the value to test. | *<math>x</math> is the value to test. | ||
*<math>sigma</math> is the standard deviation of the population. | *<math>sigma</math> is the standard deviation of the population. | ||
| − | |||
==Description== | ==Description== | ||
| Line 47: | Line 46: | ||
*[[Manuals/calci/NORMSINV | NORMSINV ]] | *[[Manuals/calci/NORMSINV | NORMSINV ]] | ||
*[[Manuals/calci/STANDARDIZE | STANDARDIZE ]] | *[[Manuals/calci/STANDARDIZE | STANDARDIZE ]] | ||
| − | |||
==References== | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Z-test Z-test] | ||
Revision as of 08:51, 12 May 2015
ZTEST(ar,x,sigma)
- is the array of values.
- is the value to test.
- is the standard deviation of the population.
Description
- This function gives the one-tailed probability of z-test.
- Z-test is used to determine whether two population means are different when the variances are known and the sample size is large.
- In , is the array of values against which the hypothesized sample mean is to be tested.
- is the hypothesized sample mean, and is the standard deviation of the population.
- When we are not giving the sigma value, it will use the standard deviation of sample.
- This function returns the probability that the supplied hypothesized sample mean is greater than the mean of the supplied data values.
- The test statistic should follow a normal distribution.
- ZTEST is calculated when sigma is not omitted and x=μ0 : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ZTEST(ar,\mu_0,sigma)=1-NORMSDIST((\bar{x}-μ0)/\frac{sigma}{\sqrt{n}})} .
- ZTEST is calculated when sigma is omitted and x=μ0:
Failed to parse (syntax error): {\displaystyle ZTEST(ar,μ0)=1-NORMSDIST((\bar{x}-μ0)/\frac{s}{\sqrt{n}})} where is sample mean , is the sample deviation and is the size of the sample.
- Suppose we want to calculate the z-test for two tailed probability then this can be done by using the Z_test function: .
- This function will give the result as error when
1. Any one of the argument is non-numeric.
2. ar or x is empty.
3. ar contains only one value.
Examples
- Example 1
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 15 | 7 | 2 | 19 | 20 | 12 |
| 2 | 3 | 4 | 8 | 1 | 10 | 15 | 5 |
- =ZTEST(A1:G1,4) = 0.00042944272036
- =2*MIN(ZTEST(A1:G1,4),1-ZTEST(A1:G1,4)) = 0.000858885440
- =ZTEST(A2:F2,10) = 0.9323691845
- =2*MIN(ZTEST(A2:F2,10),1-ZTEST(A2:F2,10)) = 0.135261630850
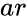 is the array of values.
is the array of values. is the value to test.
is the value to test.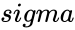 is the standard deviation of the population.
is the standard deviation of the population.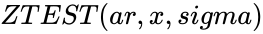 ,
,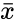 is sample mean ,
is sample mean , 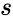 is the sample deviation and
is the sample deviation and  is the size of the sample.
is the size of the sample.
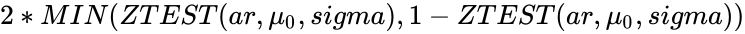 .
.