Difference between revisions of "Manuals/calci/IMLOG10"
Jump to navigation
Jump to search
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''IMLOG10( | + | <div style="font-size:30px">'''IMLOG10(Complexnumber,Base)'''</div><br/> |
| − | *<math>z</math> | + | *<math>z</math> is of the form <math>z=x+iy</math> |
| + | *<math>Base</math>is value of the base. | ||
==Description== | ==Description== | ||
*This function gives the common logarithm of a complex number. | *This function gives the common logarithm of a complex number. | ||
| − | *IMLOG10( | + | *In <math>IMLOG10(Complexnumber,Base)</math>, where Complexnumber is in the form of <math>z=x+iy</math>. i.e <math>x</math> & <math>y</math> are the real numbers. |
| − | * | + | *And <math>I</math> is the imaginary unit .<math>i=\sqrt{-1}</math>. |
| − | *Log base 10, is known as the common | + | *Log base 10, is known as the common Logarithm or Decadic logarithm, is the logarithm to the base 10. |
| − | *To find the common logarithm of a complex number we have to calculate from the | + | *To find the common logarithm of a complex number, we have to calculate from the Natural Logarithm. |
| − | *So log10(x+iy)=( | + | *So <math>log10(x+iy)=(log_{10} e)ln(x+iy)</math>. |
| − | *We can use COMPLEX function to convert | + | *We can use [[Manuals/calci/COMPLEX| COMPLEX]] function to convert real and imaginary number into a complex number. |
==Examples== | ==Examples== | ||
| − | #IMLOG10("6+7i")=0.964709462857146+0.37443569720420i | + | #=IMLOG10("6+7i") = 0.964709462857146+0.37443569720420i |
| − | #IMLOG10("4-5i")=0.806391928359868-0.389151908999031i | + | #=IMLOG10("4-5i") = 0.806391928359868-0.389151908999031i |
| − | #IMLOG10("8")=0.903089986991944 | + | #=IMLOG10("8") = 0.903089986991944 |
| − | #IMLOG10("3i")=0.477121254719662+0.682188176920921i | + | #=IMLOG10("3i") = 0.477121254719662+0.682188176920921i |
| − | #IMLOG10("0")=NULL | + | #=IMLOG10("0") = NULL |
| − | + | ||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|m-d_Xks90AM|280|center|Log of Complex Number}} | ||
==See Also== | ==See Also== | ||
| Line 24: | Line 28: | ||
*[[Manuals/calci/LOG10 | LOG10 ]] | *[[Manuals/calci/LOG10 | LOG10 ]] | ||
*[[Manuals/calci/COMPLEX | COMPLEX ]] | *[[Manuals/calci/COMPLEX | COMPLEX ]] | ||
| − | |||
==References== | ==References== | ||
| − | [http://en.wikipedia.org/wiki/ | + | [http://en.wikipedia.org/wiki/Binary_logarithm Binary Logarithm] |
Latest revision as of 13:43, 12 June 2015
IMLOG10(Complexnumber,Base)
- is of the form
- is value of the base.
Description
- This function gives the common logarithm of a complex number.
- In , where Complexnumber is in the form of . i.e & are the real numbers.
- And is the imaginary unit ..
- Log base 10, is known as the common Logarithm or Decadic logarithm, is the logarithm to the base 10.
- To find the common logarithm of a complex number, we have to calculate from the Natural Logarithm.
- So .
- We can use COMPLEX function to convert real and imaginary number into a complex number.
Examples
- =IMLOG10("6+7i") = 0.964709462857146+0.37443569720420i
- =IMLOG10("4-5i") = 0.806391928359868-0.389151908999031i
- =IMLOG10("8") = 0.903089986991944
- =IMLOG10("3i") = 0.477121254719662+0.682188176920921i
- =IMLOG10("0") = NULL
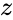 is of the form
is of the form 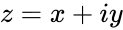
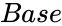 is value of the base.
is value of the base. , where Complexnumber is in the form of
, where Complexnumber is in the form of  &
& 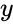 are the real numbers.
are the real numbers.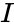 is the imaginary unit .
is the imaginary unit .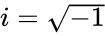 .
.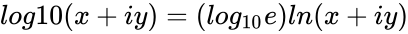 .
.