Difference between revisions of "Manuals/calci/TTESTEQUALVARIANCES"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''TTESTTWOSAMPLESEQUALVARIANCES('''Array1, Array2, HypothesizeDiff, Alpha, NewTableFlag) where, '''Array1 '''...") |
|||
| (15 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''TTESTTWOSAMPLESEQUALVARIANCES(ar1,ar2,md,alpha,lv)'''</div><br/> |
| + | *<math>ar1 </math> and <math> ar2 </math> are set of values. | ||
| + | *<math>md </math> is the Hypothesized Mean Difference. | ||
| + | *<math> alpha </math> is the significance level. | ||
| + | *<math> lv </math> is the logical value. | ||
| − | + | ==Description== | |
| + | *This function calculating the two Sample for equal variances determines whether two sample means are equal. | ||
| + | *We can use this test when both: | ||
| + | *1.The two sample sizes are equal; | ||
| + | *2.It can be assumed that the two distributions have the same variance. | ||
| + | *In <math>TTESTTWOSAMPLESEQUALVARIANCES(ar1,ar2,md,alpha,lv)</math>, <math>ar1 </math> and <math> ar2 </math> are two arrays of sample values. <math> md </math> is the Hypothesized Mean Difference . | ||
| + | *Suppose md=0 which indicates that sample means are hypothesized to be equal. | ||
| + | *<math> alpha </math> is the significance level which ranges from 0 to 1. | ||
| + | *<math> lv </math> is the logical value like TRUE or FALSE. | ||
| + | *TRUE is indicating the result will display in new worksheet.Suppose we are omitted the lv value it will consider the value as FALSE. | ||
| + | *The t statistic of this function calculated by: | ||
| + | <math>t = \frac{\bar{x_1}-\bar{x_2}}{s_{x1}.s_{x2}.\sqrt{\frac{2}{n}}}</math> | ||
| + | where <math>s_{x1}.s_{x2} = \sqrt{\frac{1}{2}(s_{x1}^2+s_{x2}^2)}</math> | ||
| + | *Here <math>s_{x1}</math> and <math>s_{x2}</math> are unbiased estimators of the variances of two samples.<math>s_{x1}.s_{x2}</math> is the grand standard deviation data 1 and data2 and n is the data points of two data set. | ||
| + | *This function will give the result as error when | ||
| + | 1.any one of the argument is non-numeric. | ||
| + | 2.alpha>1 | ||
| + | 3.<math>ar1 </math> and <math> ar2 </math> are having different number of data points. | ||
| − | + | ==Examples== | |
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C !! D!! E !! F | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 10 || 15 || 18 || 27 || 12 || 34 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 17 || 20 || 25 || 39 || 9 || 14 | ||
| + | |} | ||
| − | + | #=TTESTTWOSAMPLESEQUALVARIANCES(A1:F1,A2:F2,2,0.5) | |
| − | + | {| class="wikitable" | |
| − | + | |+Result | |
| − | + | |- | |
| − | + | ! !! Variable 1 !! Variable 2 | |
| − | + | |- | |
| − | + | ! Mean | |
| − | + | | 19.333333333333332 || 20.666666666666668 | |
| − | - | + | |- |
| − | + | ! Variance | |
| − | + | | 87.06666666666666 || 109.86666666666667 | |
| − | + | |- | |
| − | + | ! Observations | |
| − | + | | 6 || 6 | |
| − | + | |- | |
| − | + | ! Pooled Variance | |
| − | + | | 98.46666666666667 | |
| − | + | |- | |
| − | + | ! Hypothesized Mean Difference | |
| − | + | | 2 | |
| − | + | |- | |
| − | + | ! Degree Of Freedom | |
| − | + | | 10 | |
| − | + | |- | |
| − | + | ! T- Statistics | |
| − | + | | -0.5818281835787091 | |
| − | + | |- | |
| − | T- | + | ! P(T<=t) One-tail |
| − | + | | 0.28678199670723614 | |
| − | + | |- | |
| − | + | ! T Critical One-Tail | |
| − | < | + | | 0 |
| − | + | |- | |
| − | + | ! P(T<=t) Two-tail | |
| − | -- | + | | 0.5735639934144723 |
| − | + | |- | |
| − | + | ! T Critical Two-Tail | |
| − | < | + | | 0.6998120613365443 |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Related Videos== | |
| − | |||
| − | |||
| − | { | + | {{#ev:youtube|OHHhzLHakKA|280|center|TTESTEQUALVARIANCES}} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |} | ||
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/TTEST | TTEST ]] | |
| − | + | *[[Manuals/calci/TDIST | TDIST ]] | |
| − | + | *[[Manuals/calci/TINV | TINV ]] | |
| − | + | *[[Manuals/calci/TTESTUNEQUALVARIANCES | TTESTUNEQUALVARIANCES ]] | |
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==References== | |
| − | + | *[http://en.wikipedia.org/wiki/Student%27s_t-test Student's t-distribution] | |
Latest revision as of 13:03, 2 July 2015
TTESTTWOSAMPLESEQUALVARIANCES(ar1,ar2,md,alpha,lv)
- and are set of values.
- is the Hypothesized Mean Difference.
- is the significance level.
- is the logical value.
Description
- This function calculating the two Sample for equal variances determines whether two sample means are equal.
- We can use this test when both:
- 1.The two sample sizes are equal;
- 2.It can be assumed that the two distributions have the same variance.
- In , and are two arrays of sample values. is the Hypothesized Mean Difference .
- Suppose md=0 which indicates that sample means are hypothesized to be equal.
- is the significance level which ranges from 0 to 1.
- is the logical value like TRUE or FALSE.
- TRUE is indicating the result will display in new worksheet.Suppose we are omitted the lv value it will consider the value as FALSE.
- The t statistic of this function calculated by:
where
- Here and are unbiased estimators of the variances of two samples. is the grand standard deviation data 1 and data2 and n is the data points of two data set.
- This function will give the result as error when
1.any one of the argument is non-numeric. 2.alpha>1 3. and are having different number of data points.
Examples
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 10 | 15 | 18 | 27 | 12 | 34 |
| 2 | 17 | 20 | 25 | 39 | 9 | 14 |
- =TTESTTWOSAMPLESEQUALVARIANCES(A1:F1,A2:F2,2,0.5)
| Variable 1 | Variable 2 | |
|---|---|---|
| Mean | 19.333333333333332 | 20.666666666666668 |
| Variance | 87.06666666666666 | 109.86666666666667 |
| Observations | 6 | 6 |
| Pooled Variance | 98.46666666666667 | |
| Hypothesized Mean Difference | 2 | |
| Degree Of Freedom | 10 | |
| T- Statistics | -0.5818281835787091 | |
| P(T<=t) One-tail | 0.28678199670723614 | |
| T Critical One-Tail | 0 | |
| P(T<=t) Two-tail | 0.5735639934144723 | |
| T Critical Two-Tail | 0.6998120613365443 |
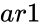 and
and 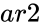 are set of values.
are set of values.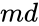 is the Hypothesized Mean Difference.
is the Hypothesized Mean Difference.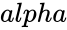 is the significance level.
is the significance level. is the logical value.
is the logical value.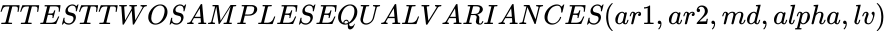 ,
, 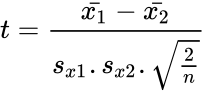
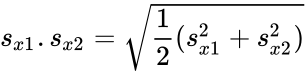
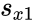 and
and 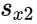 are unbiased estimators of the variances of two samples.
are unbiased estimators of the variances of two samples.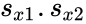 is the grand standard deviation data 1 and data2 and n is the data points of two data set.
is the grand standard deviation data 1 and data2 and n is the data points of two data set.